On considère donc deux corps de masse respective 
et 
en
orbite circulaire autour de leur centre de gravité commun O, de
période de révolution T. Nous rappelons la troisième loi de
Kepler
,
qui permet d'exprimer la période T en fonction des paramètres du
système, G dénotant la constante de gravitation universelle:
Nous considérons le référenciel tournant autour de O pour lequel les
deux corps apparaissent fixes, de coordonnées respectives: 
et 
. O étant le centre de gravité du système, on a:
Nous noterons à l'occasion 
et 
où k est
une grandeur caractéristique du système.
Un petit corps m est plongé dans le champ gravitationnel du système
décrit précédemment. Nous restreignons le problème à 2 dimensions, sur
le plan de rotation du système. Le corps m est alors repéré par ses
coordonnées (x,y) dans le
repère tournant, et par les vecteurs 
, 
et
comme décrit sur la figure suivante.
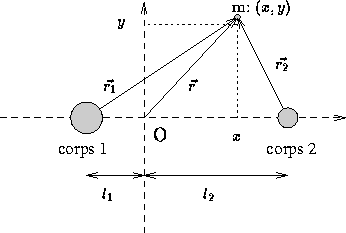
Figure 1: Repérage dans le problème à trois corps simplifié