Dynamique du système autour des points et

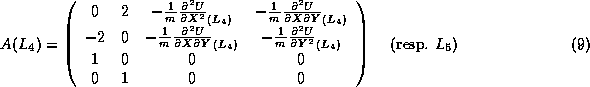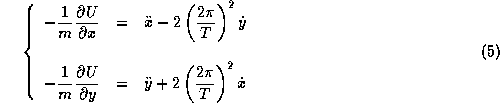
On admet que le mouvement dans le référenciel tournant est régi par le système d'équations différentielles ordinaires suivantes:

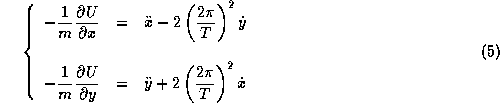
On choisit un système d'unité dans lequel on peut réécrire (avec ):

Les points et :

• Écrire dans ce système d'unité la nouvelle expression de U, ainsi que le nouveau système d'équations différentiel qui régit le mouvement du système.
• Donner, dans le nouveau système d'unité, les coordonnées du point (resp. ).
• Évaluer, toujours dans ce système d'unité, les valeurs de , et aux points et .

Linéarisation du système:

On effectue un changement de repère, utilisant les coordonnées (X,Y), de telle façon que le centre du nouveau repère se trouve en ou en posant:

On admet que le mouvement du système linéarisé autour du point d'équilibre (resp. ) vérifie le système linéaire d'équations différencielles:

• Exprimer les équations du mouvement du système linéarisé dans le nouveau système d'unité en fonction de X, Y, et de .

Stabilité du système linéarisé:

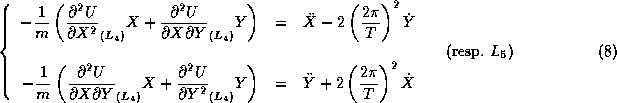
La stabilité du système linéaire est assurée si la partie réelle des valeurs propres de la matrice , définie comme suit, sont toutes simultanément négatives ou nulles.

• Calculer les valeurs propres de et de ,
• Trouver l'intervalle de valeur pour qui assure la stabilité du système linéarisé.