Calcul de l'énergie du système

L'énergie cinétique du système vaut:

> Ec := 1/2 * m* v^2;
> v := 2*Pi*sqrt(x^2+y^2)/T;
> [solve( (T/2/Pi)^2 * G * (m1 + m2) = (l1 + l2)^3, T)];
> T := simplify(op(1,"));
> eval(Ec);

Le potentiel gravitationnel vaut:

> V := - G*m1*m/r1 -G*m2*m/r2;
> r1:=sqrt((x+l1)^2+y^2);
> r2:=sqrt((x-l2)^2+y^2);

L'énergie potentielle du système vaut:

> U := - Ec + V;
> pre_AN:={m1=k*l2,m2=k*l1};
> expand(subs(pre_AN,U)/G/m/k);

Les applications numériques s'obtiennent de la façon suivante:

> AN:={l2=m1,l1=m2,m1=4,m2=1,G=1};
> UN_m:=expand(subs(AN,subs(AN,U/m)));
> plot3d(log(abs(UN_m)),x=-6..6,y=-6..6,grid=[20,20]);
> # Representation de la norme du gradient de potentiel
> grad_UN:=diff(UN_m,x)^2+diff(UN_m,y)^2;
> plot3d(log(grad_UN),x=-6..6,y=-6..6,grid=[20,20]);

  
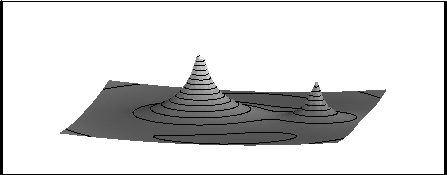
Figure 2: Potentiel gravitationnel du problème à trois corps simplifié

Position de et :

Il est acquis que l'énergie potentielle U vaut:

Les dérivées partielles valent:

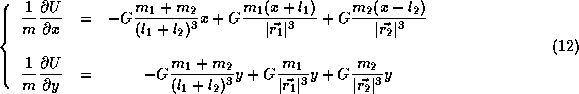
L'annulation des deux dérivées partielles impose (après simplification par G):

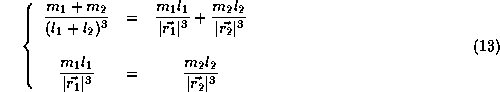
De la seconde équation, comme , on tire . La première équation permet alors de conclure ce qui clot la démonstration.