Dynamique du système

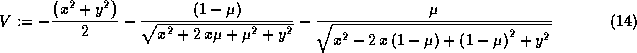
On définit un nouvelle ensemble de valeur:

> OAN  :=  {l2=m1,l1=m2,m1=1-mu,m2=mu,G=1,m=1};

Dans ce système d'unité, nous avons:

> subs(OAN,subs(OAN,(2*Pi/T)^2));
      1

> V := subs(OAN,subs(OAN,U));

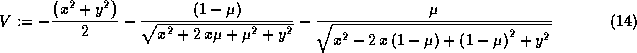
Donc le nouveau système d'équations différentielles qui régit le système est le suivant (avec V défini par l'expression précédante):

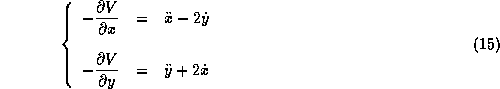
Les coordonnées des points d'équilibre sont les suivantes:

> coors[L4] :={x=-mu + cos(Pi/3),  y=sin(Pi/3)}; 
> coors[L5] :={x=-mu + cos(-Pi/3), y=sin(-Pi/3)};

L'évaluation des dérivées secondes de U en et se fait alors très rapidement:

> Vxx     := diff(V,x,x);
> Vyy     := diff(V,y,y);
> Vxy     := diff(V,x,y);
> simplify(subs(coors[L4],Vxx)); 
  simplify(subs(coors[L5],Vxx));
       -3/4     -3/4

> simplify(subs(coors[L4],Vyy));
  simplify(subs(coors[L5],Vyy));
       -9/4     -9/4

> simplify(subs(coors[L4],Vxy));
  simplify(subs(coors[L5],Vxy));
       3/4 * sqrt(3) * (2*mu - 1)      
      -3/4 * sqrt(3) * (2*mu - 1)

On peut d'ailleurs vérifier au passage que les premières dérivées partielles de U s'annullent:

> Vx      := diff(V,x);
> Vy      := diff(V,y);
> simplify(subs(coors[L4],Vx));simplify(subs(coors[L4],Vy));
          0, 0

> simplify(subs(coors[L5],Vx));simplify(subs(coors[L5],Vy));
          0, 0

Il ne reste plus qu'à définir les matrice A[L4] et A[L5], puis de calculer les valeurs propres des deux matrices:

> A[L4] := [[0,2,-simplify(subs(coors[L4],Vxx)),
  -simplify(subs(coors[L4],Vxy))],
  [-2,0,-simplify(subs(coors[L4],Vxy)),
  -simplify(subs(coors[L4],Vyy))],
  [1,0,0,0],[0,1,0,0]];

> A[L5] := [[0,2,-simplify(subs(coors[L5],Vxx)),
  -simplify(subs(coors[L5],Vxy))],
  [-2,0,-simplify(subs(coors[L5],Vxy)),
  -simplify(subs(coors[L5],Vyy))],
  [1,0,0,0],[0,1,0,0]];

> with(linalg):
> Vals[L4]:=[eigenvals(A[L4])]; Vals[L5]:=[eigenvals(A[L5])];

On constate que l'ensemble des valeurs propres des deux matrices sont identiques. En conséquence nous n'étudierons que les variations de Vals[L4]. Traçons la courbe représentative de la partie réelle des 4 valeurs propres:

> Val1:=Re(op(1,Vals[L4]));Val2:=Re(op(2,Vals[L4]));
> Val3:=Re(op(3,Vals[L4]));Val4:=Re(op(4,Vals[L4]));
> plot(Val1,mu=0..0.5,color=red);plot(Val2,mu=0..0.5,color=red);
> plot(Val3,mu=0..0.5,color=red);plot(Val4,mu=0..0.5,color=red);

  
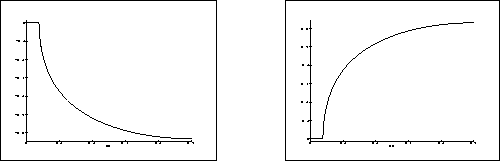
Figure 3: Partie réel des valeurs propres du système en fonction de

Approximativement, on constate que les 4 valeurs propres sont simultanément négatives où nulles si et seul si est inférieur à une valeur proche de 0.04.

Aux regards des valeurs propres, comme par exemple , il apparait que la partie réelle n'est nulle que si :

> mu_lims := [solve(1+27*mu^2-27*mu>0,mu)];

> evalf(mu_lims);

Donc, les points de Lagrange ne sont stables que si le rapport de masse entre les deux corps considérés est inférieure à .