La famille de polynome apparaît comme une définition récursive.
Toutefois la récursion n'est pas très claire, et tel quel, il est
impossible de noter sous Maple (ou n'importe quel autre logiciel de
calcul formel) ces polynomes.
La seule définition récursive (par rapport à l'indice n)
naturelle pour la famille ![]() est la suivante:
est la suivante:
![]()
![]()
![]()
La traduction en Maple de ce système d'équations se fait alors directement:
> psi := proc(n:posint ,s) if n>1 then psi(n-1,phi(n,s)) else
phi(1,s) fi end:
> phi:=(n,s)-> 1+(h-n+1)/n*X*s;
> P:=n->psi(n,1);
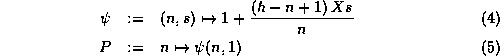
Un exemple d'utilisation nous montre que nous sommes parvenu
effectivement à définir récursivement ![]() :
:
> P(3);
![]()
On s'apperçoit que cette famille de polynome est en fait le
début du développement de Taylor au voisinnage de 0 de la
fonction ![]() .
.
> Diff_P:=P(5)-(1+X)^h:series(Diff_P,X=0,7):expand("):factor(");
![]()
Notons au passage que 720 n'est autre que 6!