Applications

Les conditions initiales correspondent à une vitesse nulle, c'est-à-dire que à l'instant t=0 les dérivées en temps de et sont nulles. Une infâme bidouille de Maple permet d'écrire automatiquement le système d'équations vérifiées par les conditions initiales:

> real_dyn_sol union diff(real_dyn_sol,t);
> cond_ini:=eval(subs({diff=0,t=0},"));

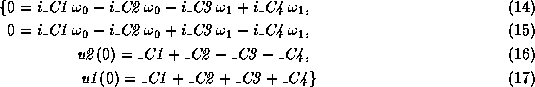
Ce système d'équation permet d'obtenir les expressions des constantes d'intégration , , et en fonction des conditions initiales. Il suffit de résoudre le système en , , et , et de reporter les solutions dans le système original (et simplifier pour faire apparaître des cosinus à la place des exponentielles complexes).

> solve(cond_ini,{_C1,_C2,_C3,_C4}):
> subs(",real_dyn_sol):
> sol:=simplify(");

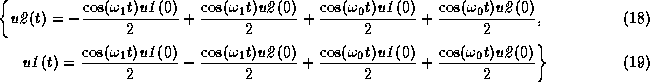
On obtient le cas particulier où les vecteurs et sont orthogonaux entre eux ainsi qu'à la direction du vecteur en prenant choisissant un système de coordonées orthogonales dans lequel les vecteurs et ont comme coordonnées respectivement et .

> sol_vect:=subs( {u1(0)=[[0],[1]], u2(0)=[[1],[0]]} ,sol);

Pour obtenir la coordonnée de selon l'axe x'Ox, il suffit de multiplier scalairement par le vecteur . La coordonnée selon l'axe y'Oy s'obtient en multipliant scalairement par . L'évaluation du produit scalaire s'obtient dans un premier temps en évaluant le produit matriciel, ce qui donne une matrice 1 1, puis en évaluant la trace de cette matrice 1 1, ce qui donne le scalaire résultant du produit scalaire des deux matrices.

> subs(sol_vect,[ [[1,0]]&*u1(t), [[0,1]]&*u1(t)]);
> map(evalm,");
> to_trace_1:=map(trace,");

Rem:

L'évaluation du produit scalaire peut également s'obtenir avec la fonction dotproduct, mais l'inconvéniant de cette fonction consiste en ce qu'elle ne prend en argument que des objets de type vector.

On a édidemment la même procédure pour obtenir les coordonnées du point .

> subs(sol_vect,[ [[1,0]]&*u2(t), [[0,1]]&*u2(t)]):
> map(evalm,");
> to_trace_2:=map(trace,");

Le tracé des trajectoires de et peut se faire en substituant les valeurs de l'application numériques dans les variables to_trace_1 et to_trace_1. En particulier, dans le cas ou , on constate que la pulsation est le double de la pulsation . La nature de la trajectoire ne dépend que du rapport entre les deux pulsation, donc pour obtenir graphiquement les trajectoire, nous pouvons prendre et . Il ne reste plus qu'à tracer (voir figure 2):

> AN:={omega[1]=2,omega[0]=1};
> plot({[op(subs(AN,to_trace_1)),t=0..Pi], [op(subs(AN,to_trace_2)),t=0..Pi]});

  
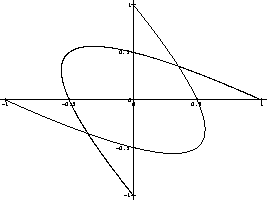
Figure 2: Trajectoires des points et