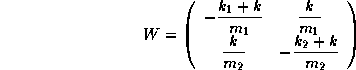Le mouvement de 
autour de sa position d'équilibre s'écrit
directement à partir de la relation fondamentale de la dynamique que
nous avons déjà écrit dans la question précédante (l'équation pour le
point 
se déduit de la même façon que dans la question précédante
en permutant les indices):
Nous nous contenterons de traduire ces deux équations en les nommant respectivement dyn_1 et dyn_2:
> dyn_1:=k_1*u1(t)+k*(u1(t)-u2(t))=-m_1*diff(diff(u1(t),t),t); > dyn_2:=k_2*u2(t)+k*(u2(t)-u1(t))=-m_2*diff(diff(u2(t),t),t);
Matriciellement, le système d'équation différentielle ordinaire précédant s'écrit de la façon suivante:
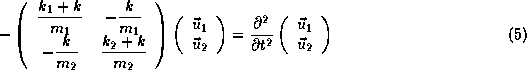
Conformément à l'énoncé, nous noterons W la matrice suivante:
> with(linalg): > W := evalm([[-(k+k_1)/m_1, k/m_1],[k/m_2, -(k+k_2)/m_2]]);
