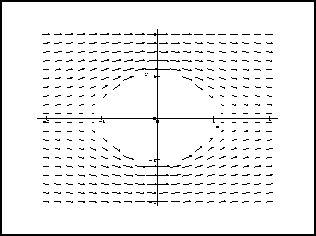
Étude du champs des vitesses

Le tracé du champs de vecteur s'obtient par exemple:

> phi :=  - v0* (r + R^2 / r) * x/r;
> cyl := Heaviside(r^2/R^2-1);
> r   := sqrt(x^2+y^2);
> phi := expand(phi):
> AN  := {v0=10,R=1}:
> phi_an := subs(AN,phi);
> cyl_an := subs(AN,cyl);
> v_an   := simplify([-diff(phi_an,x)*cyl_an, -diff(phi_an,y)*cyl_an]):
> with(plots):
> fieldplot(v_an,x=-4..4,y=-4..4);

  
Figure 2: Champs des vitesses

Pour obtenir la perpendicularité des gradients de et de il suffit de vérifier que leur produit scalaire est nul:

> psi :=  - expand(v0* (r - R^2 / r) * y/r);
> diff(phi,x)*diff(psi,x) + diff(phi,y)*diff(psi,y);
> simplify(");
                  0

Le tracé des isopotentiels s'obtient comme décrit dans le texte du sujet, en prenant bien garde de désaffecter la variable r en faisant:

> r:='r';

  
Figure 3: Lignes de courant