La distance qui sépare les deux chemins vaut exactement 
. Le calcul de la dérivée partielle par rapport à
b s'obtient astucieusement de la façon suivante:
Donc le développement au premier ordre de l(b,y) aboutit à:
L'amplitude complexe de l'onde résulte de la superposition de toutes les ondes qui ayant parcourues la distance l(b,y), sont déphasées de kl(b,y) par rapport à l'oscillation de l'original. Donc:
On introduit l'expression de la transformées de Fourier 
de
r(b):
Donc la luminosité obtenue sur l'écran est directement proportionnelle à la norme de la transformée de Fourier du motif diffractant.
Dans le cas d'une fente rectangulaire de largeur 
:
expand(convert(int(exp(-I*y*b*k/l0)/delta,b=-delta/2..delta/2),trig));
L'application numérique suit immédiatement:
lg := sqrt((y-b)^2+d2^2);
In := (sinc(y * delta * k / 2 / subs(b=0,lg)))^2;
AN := {k=966E4, delta=1E-3, d2=10};
In_AN := subs(AN,In);
plot(In_AN,y=-5E-2..5E-2);
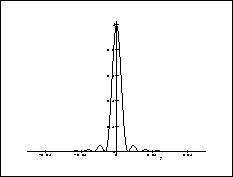
Figure 4: Franges d'interférences dues à la largeur de la fente
La généralisation à deux dimensions ne posent pas de problème. En conséquence, l'amplitude résultant de la superposition des rayon provenant d'une fente rectangulaire vaut:
R:=expand(convert(int(int(exp(-I*y1*b1*k/l0)* exp(-I*y2*b2*k/l0)/delta[1]/delta[2],b1=-delta[1]/2..delta[1]/2), b2=-delta[2]/2..delta[2]/2),trig));Ce qui donne pour l'intensité, après manipulation manuelle:
Ires :=(sinc(k*delta[1]*y1/2/d2)*sinc(k*delta[2]*y2/2/d2))^2;
AN := {k=966E4, delta[1]=5E-4, delta[2]=1E-3, d2=10};
Iran:=subs(AN,Ires);
with(plots):
plot3d(Iran,y1=-2E-2..2E-2,y2=-2E-2..2E-2);
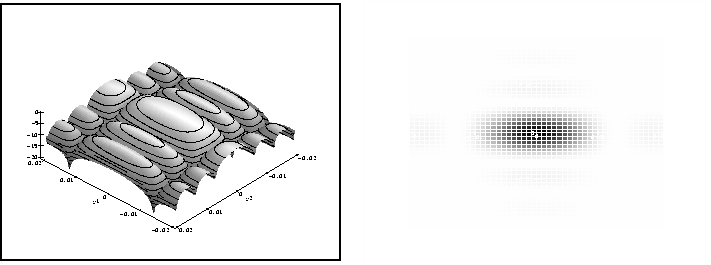
Figure 5: Franges d'interférences bidimensionnelles dues à la largeur
de la fente