Suite récurente non linéaire

Le problème consiste à identifier les solutions polynômiales de la suite définie comme suit:

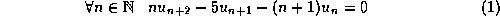
• On suppose que 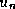est un polynôme U de degré d: 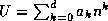. On se fixe, pour faire les calculs sous Maple, un degré d assez grand. Définir le polynôme U [sum].
• Montrer que la fonction [subs] permet d'obtenir les expressions de 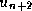puis de .
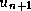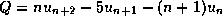• Définir le polynôme . Développer ce polynôme [expand], puis regrouper les termes selon les puissances de n [collect].
• Le polynôme U est une solution du problème si et seulement si le polynôme Q est identiquement nul, c'est-à-dire si tous ses coefficients sont nuls. Définir sous Maple l'ensemble des équations que doivent vérifier les coefficients 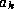pour que U soit effectivement une solution. [coeffs].
• Résoudre le système de d+1 équations à d+1 inconnues [solve] (rem: pour définir l'ensemble des inconnues, vous pourrez utiliser la syntaxe suivante: {a[k]$k=0..d}).
• Reporter les solutions 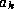dans U [subs].
• Factoriser la solution [factor].
• Conclure.