Le calcul numérique des solution peut se faire par exemple en
définissant une fonction qui, pour chaque n, évalue numériquement la
solution de l'équation 
dans l'intervalle
. La syntaxe est la suivante:
> u:=n->fsolve(tan(x)=x, x,(n-1/2)*Pi..(n+1/2)*Pi);
Il ne reste plus qu'à évaluer cette fonction en 1, 2, 3, 4 et en 10.
> [u(1),u(2),u(3),u(4), u(10)];
[4.493409458, 7.725251837, 10.90412166, 14.06619391, 32.95638904]
Le développement en série entière de 
est un peu plus
technique. Dans un premier temps nous définissons l'expression p qui
correspond à l'ordre du développement. La variable u est ensuite
utilisée pour définir le développement symbolique:
> p:=4; u:= n*Pi + Pi/2 - sum(a[k]/n^k,k=1..p);
La suite correspond à l'identification du développement asymptotique
de u avec 
(enfin plus exactement avec 
qui
est identique à ):
> collect(eval(subs(O=0,series(tan(u-n*Pi)-u,n=infinity,p-1))),n);
Il suffit de résoudre le système correspondant à tous les coefficients à 0:
> solve({coeffs(",n)},{a[k]$k=1..p});
Pour obtenir l'expression finale de u, il suffit d'introduire dans u la solution obtenue précédemment:
> subs(",u);
Ce calcul mené pour p=12 donne:
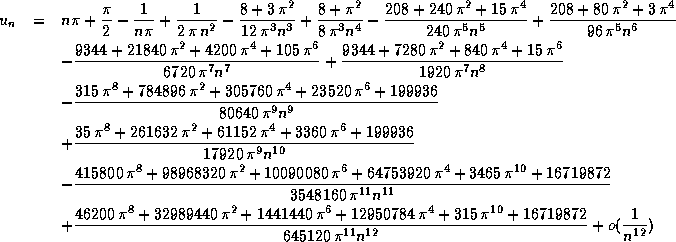
Ce qui, évalué numériquement pour n=10, donne la même valeur que nous
avions obtenue au début par une résolution numérique de l'équation
:
> evalf(subs(n=10,"));
32.95638904