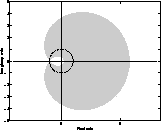
Figure 1: Unit circle inside the convergence domain of LIF.
A Lagrange Interpolator Filter (LIF) of order N and delay d consists in a FIR filter, the coefficients of which are polynomials of order N in d. A LIF has to correspond to an exact delay filter when d is integer. As pointed out in [2], it appears that any FIR filter which verifies the so called maximally flat condition is a LIF. Said differently it means that a LIF corresponds to a FIR filter, the Fourier transform of which best fits the ideal Fourier transform at zero frequency.
We shall notice that each partial series expansion of 
corresponds to the best polynomial approximation around z=1.
Thus each 
is the transfer function of the FIR
filter, the Fourier transform of which best fits the ideal Fourier
transform at zero frequency. This proves, by using the maximally
flat condition, that is the transfer function of the LIF of
order N.
LIFs are usually only used in their optimal delay range
[3] which is 
.
We state a conjecture (eq. 5) about the
convergence domain when LIFs are used in this range.
The convergence domain, 
, is
geometrically characterized by the inside of the curve (fig.
1) which parametric equations are given below
(eq. 6)):
As we can see on figure 1, the whole unit circle is contained inside the convergence domain, except for the singular point -1. This proves that an increase of the filter order improves the approximation at any frequency.
