A full discription of a music piece requires the use of both events and continuously varying parameters. However, music programs using only discrete events exist. Since most elements in common music practice, such as pitch and intensity, are discretized, a discrete description can suffice for a composition environment. The MIDI protocol uses events to send control values to synthesizers. These control values may describe typical ``continuous'' parameters such as air pressure. The rationale behind this presentation is the these parameters are slow varying and can thus be sampled at a low rate. Despite this fact, this ``pointillist'' representation makes any transformation (stretching, transposition, adding vibrato, ...) on the pitch curve difficult. Systems using only continuous functions have also been proposed [MMR74]. But when continuous functions are used to describe the start and end time of sounds, the duration of the sound is hard to express.

The need for both discrete elements and continuous functions is all the more desirable in a music environment that integrates composition and sound synthesis. Sound synthesis systems are expected to offer a rich set of continuous functions to describe the evolution of the control parameters in time. Continuous time functions describe frequency and amplitude curves, and any other variable in the synthesis algorithm that may vary in time. In this section we will consider the following issues:

• The relations between continuous time and events.

• The relation between continuous control functions and hierarchical structures.

• The manipulation of continuous time functions.

There is a close dependency between event times and continuous time functions. Event times influence the definition of continuous functions. For example, an amplitude envelope should be stretched to fit in the duration of a note. This type of relation is not always valid, however. Amplitude curves of percussive instruments are independent of the note duration. Continuous functions can also specify event times. The user may wish to express the end of a note in terms of its amplitude. As in the case where the note should stop when the amplitude drops below -60 decibels. Also tempo curves influence event times. Tempo curves are continuous functions used to introduce tempo changes and rhythmic alterations and phrasing. Continuous functions are also used to define more local stretch operations and time deformation [AK89,Dan97].

 

Figure 3.3: The local amplitude curves of the temporal objects are shaped by a global amplitude curve.

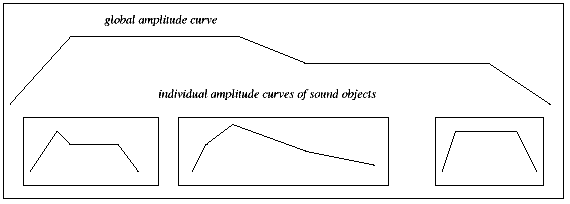
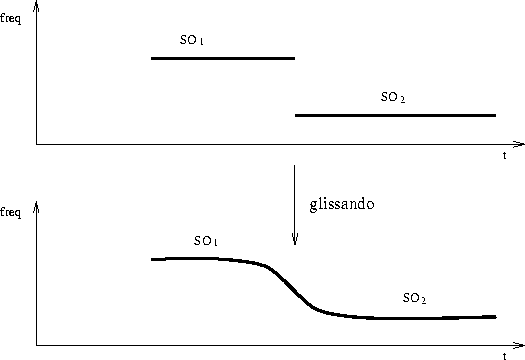
There is often a correspondance between control functions and the hierarchical structure of a piece. Control data is passed between the different levels within the piece. Classical examples are the phrasing of a group of notes. Phrasing may apply intensity and pitch changes global to all notes of the group. Several temporal objects can have a global amplitude curve shaping their local amplitudes (Fig. 3.3). In the case of the global amplitude curve, data is passed ``top-down''. There are cases in which several objects are engaged in a transformation and data is passed between objects. One of those is a portamento between two sound objects (Fig. 3.4). Pitch information of the two sound object has to be known to some higher level transformation function. In addition, the control function must anticipate the value of the second note.

 

Figure 3.4: A glissando between two temporal objects requires the acces to data local to each temporal object by a global transformation function.

Rodet, Cointe, and collegues developed an environment to control the Chant synthesizer for the singing voice. They introduced the notion of synthesis-by-rule to control the transitions between vowels and notes. In Formes a piece is represented as a tree structure of objects representing time-varying values. Rules associated with the objects calculate the output values at time intervals defined by the system. These rules are invoked by a monitor object that walks this ``calculation tree'' [RPB93, RC84]. The hierarchical structure and succesive invocation of the rules of ``parent'' and ``child'' objects gives an elegant solution to phrasing problems. The more recent Diphone project inherits the hierarchical organization for the description and interpolation of phrases from Formes but no longer offers the lisp interface [RL97].

Anderson & Kuivila also allow the hierarchical structuring of control functions. Control values are calculated in time by ``processes.'' Each process has its local virtual time space. This allows local time deformations. The values are calculated at well-defined times, often at the beginning or end of a note. They are not used for fine-grain control. Time functions are calculated incrementally: they expect the next time to be bigger than the current time. This complicates the anticipation of control values [AK89].

Also Foo, developed by Eckel & González-Arroyo, defines a rich set of constructs to define continuous control functions. In addition, time functions can be multi-dimensional. Hierarchical time contexts can be constructed. A context represents a time offset to its parent context and defines a temporal closure for all the synthesis modules in the context.

 

Figure 3.5: The vibrato problem.

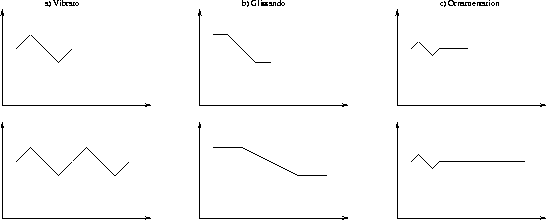
The manipulation of continuous functions for music systems brings forth its own set of problems. We will present examples taken from a series of articles written by Dannenberg, Desain, and Honing [DH92,Hon93,Hon95,Dan97,DDH97]. Consider a sound with a vibrato (Fig. 3.5 a). Vibrato is generally considered as the regular modulation of the frequency around the perceived pitch of a note. The vibrato is characterized by the frequency and the amplitude of the modulation. The frequency of the vibrato is independent of the duration of a sound object and thus invariable under time transformations such as stretching. When the sound object is stretched, more vibrato cycles are added at the end. A (sinusoidal) glissando, however, depends on the duration of the sound object. In a glissando the frequency of a note ``slides.'' Glissando should be stretched accordingly when the temporal object's duration changes (Fig. 3.5 b). An ornamentation such as the one depicted in figure 3.5 c) has a constant duration. It is not stretched, and no cycles are added at the end. The representation and handling of these different behaviours is known in the literature as the vibrato problem. They can be considered as equivalents of the drum-roll and grace note problem, discussed earlier, in the organization of discrete elements. In the vibrato problem, the behavior of the stretch transformation is local to the temporal object. In the case of the global amplitude curve or the portamento, structures on a more abstract level are engaged in the transformation.

Dannenberg developed a series of composition systems. Chronologically, these are Artic, Canon, Fugue, and Nyquist [DR86,Dan89,Dan93]. Artic and Fugue do not handle sound synthesis but provide a rich framework to define continuous values for the control of sound synthesis. In Fugue and its successor Nyquist, sound synthesis can be handled. In these environments basic musical elements can be combined into composite structures. The musical elements have a body and a transformation environment. For example, the body of a note structure contains its pitch and duration. The transformation environment contains transformation data such as stretch values. Time functions and transformations can refer to this environment parameters (see also [Hon95]).

Honing & Desain have defined a framework both for the composition of discrete musical elements and continous control functions. Both elements can form alternating layers of discrete and continuous information [DH92,Hon93]. They propose the use of ``generalized time functions.'' These functions are defined as functions of three arguments: the actual time, a start time, and a duration. Generalized time functions can be combined, or passed as argument to other time functions. They can be linked to a specific musical attribute such as pitch or amplitude. Since the time context of a control function is available, solutions to the vibrato problem can be expressed elegantly.