In this section we will give a formal description of a multimedia system. This formal description is not meant as a rigid mathematical theory. In this section we will express the concepts of the environment in a concrete notation. This model is intended as a guideline for the implementation. We can briefly describe the system in words as follows.

1.

The system produces a series of output values at regular time intervals. In the case of a sound system, the output is a sample frame or a buffer of sample frames. The output value is calculated by a set of synthesis processes. Each synthesis process is a program and its output depends on the state of the system.

2.

At any time events may arrive. These events change the state of the system according to some program. By changing the state of the system, the events influence the output values calculated by the synthesis processes.

We will precise these ideas below. Let us start with a more precise definition of events. Let P_n be the set of n-ary functional symbols, called programs, P_n = {p_i}, n,i in N, n ≥ 0. We will call P = U P_n the set of programs. Furthermore, let V be the set of anything.

Using the previous definitions, we can now define the synthesis system as follows.

We will call the state of the system S = (T, p_i, o, SP, E, V) the quadruple (o, SP, E, V). The state of the system can change thru the application of a program p with arguments a. In particular, the program p can create and insert new events in the system. To simplify the notation in the following discussion we will notate the set of events created by the program p as E_p. We notate the application of a program p as follows:

In the previous paragraph we gave the definition of the elements of our system. We will now see how the system evolves. We assume that external to the system there exists a clock that indicates the precise time t. The system then follows three rules:

Rule 1 (Initialization)  

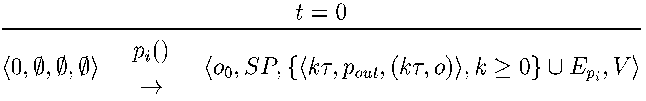
Rule 1 describes the initialization. It is applied when the time equals zero. First, the set of events E is made equal to the set of all synthesis events. These synthesis events schedule the evaluation of the synthesis program p_out after every interval T. The arguments to p_out are the time kT and the output o of the system. Then the initialization program p_i is evaluated. p_i defines the initial state of the system and can create additional events and synthesis processes. After initialization the system evolves according to rules 2 and 3.

Rule 2 (Synthesis)  

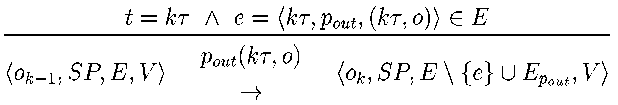Rule 2 describes the synthesis task. The synthesis is triggered by the synthesis events (kT, p_out, (kT, o)). When the time equals kT the output program is evaluated. The main purpose of the program p_out is to calculate a new value for the output o. However, it can also modify the state of the system and insert new events in E.

Rule 3 (Event handling)  

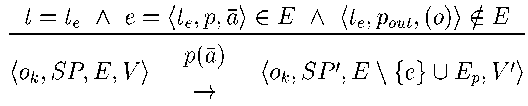Rule 3 describes the event handling. If at time t = t_e there exists an event e = (t_e, p, a) the program p of the event is evaluated with the arguments a. The program p can change the state of the system and schedule new events. If an events exists at the same time of a synthesis event, the synthesis event is handled first.

The output o of the system is updated by the output program p_out at times kT. Let o_k be the value of o after the evaluation of p_out at t = kT.

Definition 3 (Output series)   The output series O of the system is the series of successive output values o_k, or O: o₀, o₁, ... , o_n, ....

For both sound and animation it is advantageous to think of the output of the system as the combination of the output of several, simultaneous sources, objects, or activities. Each activity represents one easily definable element in the total output. Moreover, each activity can start and stop at any time. Thus, at any time any number of simultaneous activities can exist. A synthesis process describes the action performed by one such single activity. It is modeled as a program sp in P₂. The application of the synthesis process modifies the value of the output o given as argument. The final value of the output of the system is a combination of the effect of all active synthesis processes. The program p_out describes the combined effect of all the synthesis processes. The order in which the synthesis processes are evaluated depends on the domain. For a graphical system the order depends on the visual hierarchy of the graphical objects and/or layers. For a sound synthesis system the output values are mixed (added) together.

During the execution of a piece, synthesis processes can be inserted or removed from the set of active synthesis processes. This insertion or removal is the result of the evaluation of an event. For convenience, we will introduce the programs add and kill. They are defined as follows: add(sp): SP<-SP U {sp} and kill(sp): SP<-SP \ {sp} Similarly, we will call an event e = (t, p, a) an add-event (kill-event) if p = add (p = add).

We will implement the model described above in a framework combined of the Java environment enriched with an embedded Scheme interpreter. Since the synthesis processes perform all the signal processing code, they should be as optimized as possible. We will develop them in the Java language because it provides better performance than Scheme code. Events have less stringent time requirements than the synthesis processes. The programs carried by the events can be written in Scheme. How the system is changed in response to events can be defined thru the Scheme interpreter. Although synthesis processes are written in Java, they can, however, request the evaluation of Scheme procedures by sending events. This is the case for schedulers, which provoke the evaluation of events program at their given times.

The Scheme interpreter typically uses a table to store the defined procedures and variables. This table is typically called the environment. Looking back at the model described above, we see that this environment corresponds to the environment V of the system. Thru the Scheme shell the user defines and manipulates variables defined in the environment. Since, the synthesis processes depend upon those variables, the user can interact with the synthesis processes thru the shell.

In our model, we deliberately neglected one element that is crucial for the implementation: the evaluation of a program takes time. In this model the evaluation of a program p is assumed to be instantaneous. Since our multimedia system is time bound and the hardware on which it runs has limited resources (limited CPU power), we will have to consider the duration of the evaluation. There exist scheduling algebras that take into account the duration of operations (see for example [vGR98]). The complexity of the model would increase unnecessarily if the notion of duration was included. Instead we will consider this duration in the practical situation of the implementation. We will see how both the synthesis and the event handling will be modeled as concurrent tasks. In chapter 7 we will discuss the time behavior of these tasks.

Besides an interface we have to provide the user with additional language constructs and data structures to organize a music piece. Just programs and events is too austere to express the complex structure of a multimedia piece. We need tools to organize data and specify the structural relationships that exist between the elements of the piece. These data structures will be discussed in chapter 5 and chapter 6.