Theoretically, with the use of computer, any sound can be produced. The digital representation of a sound, however, asks for an enormous amount of data and it is therefore inconceivable to generate this data by hand. To describe and facilitate the generation of sound synthesis algorithms are used. A pure sound, for example, can be generated as follows:

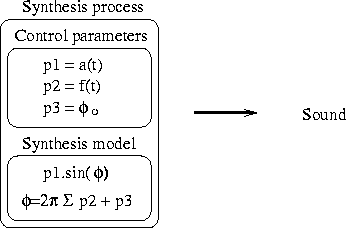
We can distinguish two parts in the expression above: the synthesis model, and the control parameters. The synthesis model defines the behavior of the synthesis process under various inputs and determines the characteristics of the sounds that can be produced. The control parameters steer the model to generate one specific sound. For a pure sound we can isolate three control parameters: p₁ = a(t), p₂ = f(t), and p₃ = phi₀. The amplitude envelop a(t) and the frequency contour f(t) are continuous functions in time. The initial phase phi₀ is a real number. The model is described by s(t) = p₁sin(phi(t)), and phi(t) = p₃ + 2.PI ∫ p₂dt. All sounds produced by the model will be pure sounds. The sound characteristics that we can ``compose'' are the pitch contour and the amplitude envelope. (The critical reader will immediately imagine complex control functions with which the output will not be a pure sound. In this introduction, for the sake of conciseness, we will accept slowly varying control functions.)

 

Figure 4.2: To produce sound we need the combination of a synthesis model and control parameters. We will call the combination of the model and the parameters a synthesis process.

We will call the combination of a synthesis model and the control parameters a synthesis process (Fig. 4.2). The activation of a synthesis process will generate a sound signal. Calling a synthesis process with a time value t will return the value sp(t) of the synthesis model at that time. For digital sound, synthesis processes are called at discrete times, multiples of the sampling period T_s: sp(nT_s). For efficiency, synthesis processes are not called for every sample, but for an array of N samples. In the latter case, the array of samples is passed as argument: sp(nNT_s,out).

The system would be quite incomplete if we allowed only one synthesis process to be active at one time; the system therefore accepts several simultaneous synthesis processes. Furthermore, a synthesis process necessarily starts and ends at some point in time. We will say the synthesis process is alive or active during a certain laps of time. We do not want to impose any restrictions on the start and end time. The live span of a synthesis processes can be very short, or can take the full length of the composition. The start and end time, together with the parameters of the synthesis process, can be known before the execution. This is the case when the system performs a composed piece. In an interactive set-up, however, these elements can be determined or modified in runtime by user intervention. Discrete user input is called an event and provokes some action on the side of the system. The action that needs to be taken is described by a program. The side effects of the evaluation of a program can be trivial, such as stopping a synthesis process. However, programs can also perform complex tasks, such as a complete reconfiguration of the system or the generation of a part of the composition. In this text we make extensive use of the concept of program. It is loosely defined as a series of instructions to perform a task, given a number of arguments. We accept, for example, that programs implements synthesis models or create new data structures. In the next section we will formalize these ideas.