(Chaos, et Composition Musicale)
RÉSUMÉ: Ce papier est une réflexion
artistique et théorique sur l'utilisation de modèles mathématiques,
notamment les modèles chaotiques et la notion de système,
en composition musicale assistée par ordinateur.
1. Introduction
Il n'existe pas, actuellement, beaucoup d'études sur les relations
entre les caractéristiques conceptuelles et techniques des modèles
mathématiques ainsi que sur l'écriture musicale qui se dégage
par leur utilisation. En ce qui concerne, notamment, l'utilisation des modèles
chaotiques, et même la notion de système, la vision de la plupart
des compositeurs est encore très naïve. Ces modèles sont
souvent utilisés soit comme des algorithmes compositionnels, soit
comme des stimuli métaphoriques, pour l'imaginaire du compositeur,
liés fréquemment aux images mentales suggérées
par les mots "chaos" et "aléatoire" et par les
"belles" représentations graphiques des orbites produites
par ces systèmes.
Ces remarques ne veulent pas être des jugement de valeurs sur les
musiques ainsi produites[1], mais veulent
seulement montrer la méconnaissance qu'il existe, de la part des
musiciens, au sujet des potentialités de ces modèles.
Finalement, notre but est de montrer l'existence de liens possibles entre,
d'un côté des modèles formels calculables, comme par
exemple les modèles non linéaires (dits du chaos) et de l'autre
côté la composition et la conceptualisation musicale. Cette
étude se fera dans le cas spécifique de la Composition Musicale
Assistée par Ordinateur, où la notion de modèle[2]
prend le sens d'instrument de formalisation ou de médiateur entre
le monde conceptuel du compositeur et le monde numérique de l'ordinateur.
Pour ces réflexions nous avons choisi d'utiliser comme toile de fond
la composition de Lambda 3.99, pièce pour guitare et synthétiseur
MIDI[3].
2. Les bases théoriques
2.1 La notion de système dynamique
Nous définirons un système dynamique à états
discrets S comme étant l'entité qui possède,
* Une fonction de transition G, qui détermine à chaque
instant l'état dans lequel se trouve le système. G
est fonction du temps:
G =>G (t)
e
* Un ensemble finit E, des états possibles que le système
peut assumer, où et désigne l'état du système
au moment "t" calculé à partir de la fonction
G.
Chaque état ei, peut être considéré
comme étant une classe d'équivalence, pouvant être à
son tour un système avec ses propres états et ses fonctions
de transition.
Un système dynamique à états discrets finis, S
, sera alors défini comme étant l'ensemble formé par
une fonction de transition G (t) et un ensemble d'états E
:
2.2 Les modèles dynamiques non-linéaires (chaotiques)
Nous appellerons de "modèle dynamique non-linéaire"
tout modèle, avec rétroaction, de la forme
où la fonction ![]() n'est pas linéaire, c'est-à-dire n'est
pas de la forme
n'est pas linéaire, c'est-à-dire n'est
pas de la forme ![]() .
.
Nous allons utiliser dans notre étude une équation qui est
un classique dans les études sur la théorie du chaos, l'équation
logistique:
variation de l'équation de Verhulst :
Cette équation (l'équation de Verhulst) a servi de modèle
dynamique pour la croissance de populations. Il s'agissait d'un formalisme
proposé par le mathématicien belge Pierre François
Verhulst (en 1838 ) pour traduire mathématiquement la thèse
de Adolphe Quetelet [4] :
"Si le développement a lieu au milieu d'obstacles qui tendent
à l'arrêter et qui agissent d'une manière uniforme,
c'est-à-dire si l'état social ne change point, la population
n'augmente pas d'une manière indéfinie mais elle tend de plus
en plus à devenir stationnaire."
Cette citation s'oppose frontalement à la thèse malthusienne
de croissance exponentielle des populations, qui n'est , en fait, qu'applicable
au cours de périodes de forte expansion d'une population, tel comme
la colonisation de terres vierges.
Beaucoup plus tard (1976) ce même modèle sera repris par Robert
M. May dans son célèbre article "Simple mathematical
models with very complicated dynamics" dans la revue "NATURE"[5].
Un fait important pour la compréhension du fonctionnement de ces
modèles est de se rendre compte qu'ils sont des résolutions
numériques d'équations différentielles. L'équation
de Verhulst présentée, n'est que la forme issue de l'algorithme
d'Euler pour résolution d'équations différentielles
de première ordre avec un incrément temporel égal à
1 (un)[6]:
pour ![]() .
.
Une bonne partie des caractéristiques, dites chaotiques, de ces modèles
dérive de l'utilisation de méthodes numériques pour
leur résolution.Cela signifie que, ce sont des systèmes très
sensibles aux erreurs d'approximation. L'équation de Verhulst
en est un bon exemple. Pendant que sa résolution par des méthodes
numériques diverge pour certaines valeurs de ![]() (entre 2.1 et
3.0), sa résolution analytique présente la solution explicite:
(entre 2.1 et
3.0), sa résolution analytique présente la solution explicite:
qui converge vers "1" quand t tend à l'infini!
Nous n'allons pas nousétendre sur la description de ces modèles
vu l'existence de bon nombre d'ouvrages vers lesquels le lecteur intéressé
pourra se diriger.
3. Les modèles chaotiques, caractéristiques et potentialités
(l'équation logistique)
Ce qui nous intéresse, en premier lieu, c'est de pouvoir étudier
certaines caractéristiques de ces modèles pour pouvoir saisir
comment elles pourront nous aider à formaliser, ou représenter
certains concepts musicaux. L'intérêt principal n'est pas de
dresser un catalogue complet de propriétés, ce que par ailleurs
nous pouvons trouver dans les textes techniques spécialisés,
mais de montrer comment nous pourrons représenter et formaliser des
concepts musicaux en utilisant quelques unes de ces caractéristiques.
3.1 Sensibilité aux conditions initiales
La caractéristique la plus importante est la sensibilité aux
conditions initiales. Ces systèmes sont très sensibles aux
erreurs. Il est possible de calculer un coefficient d'amplification des
erreurs, pour chaque itération, par la mesure de l'exposant de Ljapunov[7].
Pour l'équation logistique ce coefficient est de 0.693. Étant
ce coefficient, "grosso-modo", le logarithme du coefficient d'amplification
des erreurs nous pourrons dire qu'à chaque itération les petites
erreurs sont, en moyenne, multipliées par deux ( ![]() ).
).
Voici une représentation graphique de l'évolution des différences
entre les valeurs générées par deux équations
logistiques avec lambda = 4.0, valeur initiale égale à 0.1
et une différence initiale de ![]() .
.
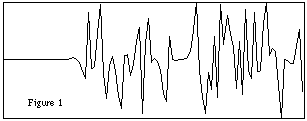
Le comportement de cette équation n'étant pas linéaire
il n'est pas possible de prévoir le décalage entre les deux
systèmes pour une erreur initiale donnée. Il semble paradoxale
qu'un système déterminé puisse présenter des
"indéterminations", puisque pour pour une même valeur
initiale, pour un même paramètre lambda et pour un même
environnement[8] la série sera totalement
déterminée[9].
3.2 Les points stables:
Pour pouvoir bien comprendre d'autres caractéristiques telles que
l'existence des "points stables" une représentation géométrique
du processus d'itération sera fort utile. Soit la résolution
numérique du système
cette résolution peut être vue comme étant une "interaction"
entre la fonction
a) ![]() et la fonction
et la fonction
b) ![]()
puisque la rétroaction peut se représenter géométriquement
comme étant un transfert d'informations entre ces deux équations.
En regardant la figure 2 nous pouvons remarquer que les deux fonctions `a' et `b' se coupent en deux points : (0 , 0) et (0.75 , 0.75). Ces deux point constituent ce que nous appelons des points stables du système puisque au moment qu'ils sont atteints le système y reste: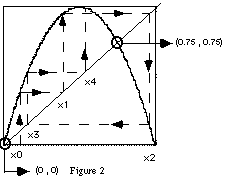
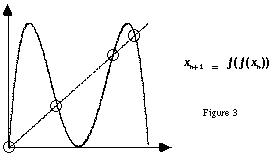
La connaissance de l'existence de ces points pourrait être très
importante du point de vue musicale. Comme nous le verrons ensuite, ces
points sont la cause de l'apparition de certaines régularités
et certaines morphologies qui pourraient être utilisés pour
organiser le matériau musical.
3.3 l'existence de symétries (égalités spatiales)
dues à l'existences des "points stables" (visualisation
géométrique)
Une bonne partie des caractéristiques dites "chaotiques"
de certains systèmes non-linéaires vient du fait qu'ils sont
des résolutions numériques d'équations différentielles,
ce qui veut dire en d'autres termes que nous essayons d'atteindre la résolution
par des approximations et non par des resolutions explicites. A chaque itération
il existe l'introduction d'une erreur d'approximation dûe au fait
que nous travaillons avec des nombres flottants et avec des machines numériques.
Pratiquement ceci veut dire qu'il est très peu probable que le système
atteigne la valeur exacte de 0.75 (ce qui dépend bien sûr de
la valeur initiale). Lorsqu'une valeur très proche de 0.75 est atteinte
le système "tourne", pour ainsi dire, autour du point (0.75
, 0.75) et diverge aussitôt. L'introduction de "petites"
erreurs à chaque intéraction empêche le système
de converger.
En regardant une représentation graphique d'une série de valeurs
générées par l'équation logistique (lambda =
4.0, x0 = 0.75), nous pouvons remarquer que cette propriété
finit par générer des symétries (au sens d'égalités
spatiales) dans l'ensemble des valeurs générées (voir
figure 4).
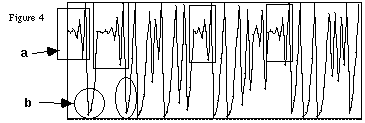
Nous remarquerons, avec un certain étonnement, que finalement
les valeurs générées par un système dit chaotique
sont plutôt "thématiques"! Il existe une répétitions
non-régulière de certains schémas morphologiquement
typés. Dans la figure 4 nous pouvons repérer deux de ces schémas.
Un premier (a) dû à l'oscillation autour de la valeur de 0.75
, et un deuxième autour du point 0.0.
3.4 D'autres propriétés
Ils existent d'autres caractéristiques, dont nous ne parlerons pas
ici, telles que "les attracteurs étranges", les "intermittences",
etc.., sur lesquelles il y a encore beaucoup de recherche à faire.
4. La conceptualisation et formalisation musicale
La question maintenant est: Comment faire le lien entre ces caractéristiques
mathématiques et des possibles utilisations musicales? Quels sont,
enfin, les liens possibles entre une conceptualisation musicale et une formalisation
logique?
Pour essayer de comprendre cela, voyons de plus près l'application
de ces concepts à la composition de la pièce Lambda 3.99 pour
guitare et synthétiseur.
4.1 La conceptualisation musicale (polyphonie virtuelle)
Dans le cas de Lambda 3.99, une des idées clés était
le concept de polyphonie virtuelle.
Il est possible, à partir d'un jeu strictement séquentiel,
de simuler une polyphonie, c'est-à-dire de faire le système
auditif associer certains événements dans le temps, et dans
l'espace des hauteurs, de façon à construire des flux auditifs
(se rappeler des suites, sonates et partitas pour instruments seuls de J.S.Bach).
Dans ce cas précis ce concept serait alors appliqué non à
la note isolée, mais à des structures plus complexes.
Nous savons, même si seulement par l'intuition, que les effets perceptifs
d'un son, d'une séquence ou d'un objet musical quelconque dépendent
du contexte musical dans lequel il s'inscrit. La perception de plusieurs
paramètres musicaux associés à un son, tel que la hauteur,
le timbre, l'intensité, l'articulation, la durée, le tempo,
etc. sont largement influencés par les caractéristiques des
sons qui le précèdent, qui coïncident avec lui et même
avec ceux qui le suivent dans le temps. Il est possible, alors pour le compositeur,
de se servir de ce phénomène et de constituer des flux musicaux.
Un "flux" est une organisation psychologique qui représente
mentalement une source physique comme une séquence d'événements
acoustiques émanant d'un même endroit.[12]
, et possédant une certaine cohérence ou continuité
interne, ce qui permettra à cette séquence d'être interprétée
comme un tout. Un des points importants pour le compositeur est de savoir
quand s'opère la scission d'une séquence en flux plus petits.
Quels sont les paramètres à manipuler?
McAdams[13], nous montre que la formation
de flux est conditionnée par certains facteurs:
-Les grands écarts au niveau des fréquences induisent le système
perceptif à grouper des événements par registres.
-Plus le tempo est rapide, plus le degré de rupture ou de décomposition
de la séquence en flux plus petits est grand.
-Des discontinuités timbriques induisent aussi la formation de flux.
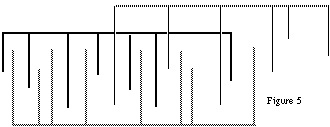
C'est à partir de ces données que nous avons formalisé
et construit une dizaine de gestes de base qui devrait permettre à
l'audition de les grouper et constituer des flux auditifs qui se superposent
virtuellement. Pour cela chaque geste a été construit de façon
à posséder certaines caractéristiques propres:
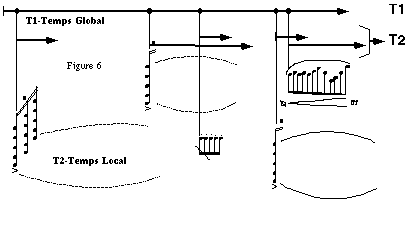
4.3 Polyphonie virtuelle et système
En fonction du cadre que nous venons de définir, nous avons généré
une polyphonie virtuelle par le séquencement de petits gestes, indexés
à des états d'un système dynamique à états
discrets, où notre fonction G sera de la forme,
L'utilisation de l'équation logistique comme fonction de transition
semblait être un bon choix. Certaines des propriétés
vues, comme les symétries et les morphologies dues aux points stables,
pourraient être utiles pour organiser l'évolution des gestes
de base. Une fonction de transition qui génère des schémas
semblables avec une oscillation entre répétition et renouveau,
nous permettrait non seulement d'avoir un ensemble de données organiques
mais aussi simuleraient, en quelque sorte, une des caractéristiques
de l'acte compositionnel, c'est-à-dire, d'être un processus
qui essaye toujours d'avancer en ayant des traces du passé et en
introduisant progressivement des éléments nouveaux. Ceci pourrait
bien fonctionner pour une période courte de temps, mais nous nous
trouverions vite confrontés à une certaine immobilité.
Il faut alors donner une direction (un sens) à l'évolution
de ce système. Pour résoudre ce problème la fonction
de transition G a été modifié ,
avec
![]() , comme condition initiale
, comme condition initiale ![]() et
et ![]() [17]
[17]
où ![]() est une fonction de contraction et
est une fonction de contraction et ![]() est une fonction
de décalage.
est une fonction
de décalage.
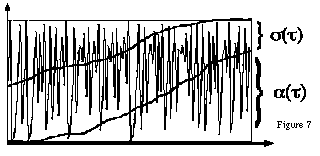
Ceci revient à appliquer deux fonctions ![]() et
et ![]() [18]
sur l'ensemble des valeurs générées de manière
à donner une direction à l'évolution du système
(figure 7). Même si ce que nous pouvons affirmer est que la transformation
que nous avons appliqué à la fonction
[18]
sur l'ensemble des valeurs générées de manière
à donner une direction à l'évolution du système
(figure 7). Même si ce que nous pouvons affirmer est que la transformation
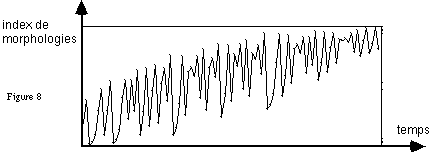
que nous avons appliqué à la fonction ![]() (qui gère
l'évolution des index de morphologies), n'est que localement linéaire,
la structure résultante présente encore des morphologies analogues
à celles générées par les "points stables",
mais ayant en même temps une direction dans l'espace des index (figure
8). Ce type de procédure a été utilisé dans
toute la pièce pour créer un processus d'évolution
en transformation continue; soit pour contrôler l'évolution
des index des gestes, soit pour contrôler l'évolution de chaque
geste[19]. La partie électronique
étant une partie de l'évolution du système et non seulement
un accompagnement de la partie instrumentale.
(qui gère
l'évolution des index de morphologies), n'est que localement linéaire,
la structure résultante présente encore des morphologies analogues
à celles générées par les "points stables",
mais ayant en même temps une direction dans l'espace des index (figure
8). Ce type de procédure a été utilisé dans
toute la pièce pour créer un processus d'évolution
en transformation continue; soit pour contrôler l'évolution
des index des gestes, soit pour contrôler l'évolution de chaque
geste[19]. La partie électronique
étant une partie de l'évolution du système et non seulement
un accompagnement de la partie instrumentale.
Un bon exemple de l'utilisation de cette procédure est la partie
centrale de Lambda 3.99, où le processus commence avec une séquence
mélodique :
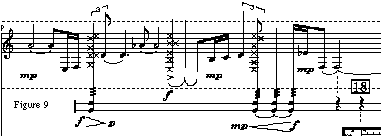
et évolue, en passant par d'autres "gestes"[20],

jusqu'à arriver à des accords "rasgado":
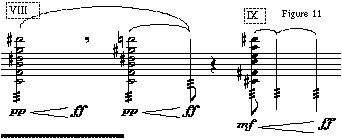
Dans notre cas précis, chacune de ces formes définissait
une classe d'équivalence, ceci pour éviter la répétition
et favoriser une perception d'évolution de chaque forme. Par exemple
sur un geste "note répétée" la forme choisie
n'était pas toujours la même. Il existait un ensemble de base
qui définissait la classe "note répétée",
comme le montre la figure 12.

Évidement les gestes n'étaient pas pris dans l'ordre linéaire
de leur "évolution" comme défini dans l'ensemble
de base, mais dans un ordre similaire à l'évolution globale
des formes, cela revient à dire que pour chaque forme nous avions
défini un ensemble d'états (générés à
partir d'une évolution linéaire du geste) et une fonction
de transition G comme pour l'évolution globale, transformée
avec des fonctions de compression et décalage.
5. Conclusion
L'important, de notre point de vue, n'est pas d'avoir trouvé des
correspondances universelles, mais de vouloir attirer l'attention vers une
utilisation des modèles mathématiques, spécialement
en ce qui concerne la composition assistée par ordinateur, qui tienne
compte d'une conceptualisation musicale. Une attitude que nous tenons à
éviter est de conférer aux modèles et aux symboles
un privilège par rapport aux processus qu'ils représentent,
ce qui voudrait dire en d'autres termes qu'une logique formelle n'implique
pas forcément en une logique musicale. Un modèle mathématique
ne peut être utilisé en composition musicale que si il est
soutenu par une conceptualisation et une pensée musicale.
Appliqué à l'expérience que nous venons de décrire,
ceci voudrait dire que les propriétés morphologiques de l'ensemble
de valeurs, générées par l'équation logistique,
n'ont pas de signification musicale si elles sont déconnectées
d'une réalité perceptive. Cet ensemble numérique n'a
pris sens qu'au moment qu'il a été utilisé pour formaliser
des notions comme celles de la mémoire au sein d'un processus musical.
Les morphologies, créées par le phénomène des
"points stables", ont été utilisées pour
créer des relations, dans le temps, entre le matériau musical
qu'elles contrôlaient, soit les gestes. De cette manière la
répétition irrégulière des morphologies a été
associée à ce mouvement qui opère dans la composition
où chaque choix est préparé par des sélections,
d'autres choix, et des explicitations antérieures opérées
à plusieurs niveaux, du plus élémentaires au essentiel.
Ainsi chaque choix doit aussi préparer les choix suivants, chaque
choix a une mémoire et il est prémonitoire[21].
Nous pourrions dire que cette caractéristique a été
utilisée pour essayer de formaliser la mémoire dans un processus
musical.
D'autre part, nous avons aperçu une émergence de nouvelles
formes par l'association de deux ou trois gestes. Les symétries contenues
dans l'ensemble de valeurs générées par l'équation
logistique ont contribué à faire ressortir de nouvelles configurations,
par la répétition de certaines séquences (par exemple
"note répétée", "séquence statique",
etc.) qui ont gagné à leur tour une vie propre. Du fait d'avoir
appliqué des transformations à la fonction de transition,
en donnant une direction au processus, ces "nouvelles configurations"
finissent elles aussi par évoluer en suivant l'évolution des
schémas graphiques (voir figure 8).
En ce qui concerne la notion de système le problème est le
même. Cette notion a été aussi utilisée pour
formaliser une des hypothèses de base de notre travail : "tout
processus musical peut être analysé comme étant l'évolution
de plusieurs formes indépendantes, ayant chacune une évolution
propre"; et pour permettre de représenter le concept que nous
avions nommé de "polyphonie virtuelle.
Finalement, le sens qui se dégage par l'utilisation d'un modèle
mathématique, en composition musicale, est la conjonction d'un ensemble
de facteurs, tels que les concepts musicaux qu'il est censé représenter,
la manière dont l'ensemble des paramètres a été
conduit dans le temps, et sans doute le contexte esthétique du compositeur.
Cependant, il nous a paru clair que les seules caractéristiques d'un
modèle ne sont une condition suffisante pour créer un sens
musical.
La connaissance des caractéristiques et du comportement d'un modèle,
de même que la connaissance des caractéristiques d'un instrument
musical, sont importantes pour pouvoir l'asservir à la pensée
et non pour asservir cette pensée au joug d'un système formel
quelconque.
6. Bibliographie
[BARNSLEY 1988] BARNSLEY Michael (1988)- Fractals Everywhere, Academic
Press, Inc.
[BIDLACK 1992] BIDLACK, Rick (1992)- "Chaotic Systems as Simple
(but complex) Compositional Algorithms", in Computer Music Journal,
vol 16, ndeg. 3, Fall 1992.
[CVITANOVIC 1989] CVITANOVIC, Predrag (1989)- Universality in Chaos,
Adam Hilger, Grande -Bretagne.
[DALMENICO 1992] DALMENICO, A. D. ; CHABERT, J. L. et CHEMLA, K. (sous la
direction de) (1992) - Chaos et Déterminisme, Ed. du Seuil,
Paris.
[DI SCIPIO 1990] DI SCIPIO A. (1990) - Composition by Exploration of
Non-Linear Dinamic Systems, in ICMC Procedings 1990.
[GOGINS 1991] GOGINS M. (1991) - Iterated Functions Systems Music,
in Computer Music Journal, vol 15, ndeg. 1 1991.
[MALT 1994] MALT, M.(1994), "Modêlos Matemáticos e
composição Assistida por Computador, Sistemas Estocásticos
e Sistemas Caóticos", in Primeiro Simposio de Computação
e Música, Caxambu, MG, Brésil.
[MALT 1993] MALT, Mikhail (1993)- Introduction à Patchwork
, IRCAM, Paris, France.
[MALT 1994] MALT, Mikhail (1994)- Chaos-librairie de modèles chaotiques
et de fractales , IRCAM, Paris, France.
[MALT 1996] MALT, Mikhail (1996) - Le compositeur et ses modèles
, Conférence dans le cadre du IIe Congrès International d'Ontologie",
sous le patronage de l'UNESCO, San Sebastian, Espagne.
[MAY 1976] MAY Robert M. (1976) - Simple mathematical models with very
complicated dynamics in Nature , vol 261 ndeg. 5560 pp. 459-467; in
[CVITANOVIC 1989]
[MAYER-KRESS 1992] MAYER-KRESS G., BARGAR R., CHOI I. (1992) - Musical
Structures in Data from Chaotic Attractors, Center for Complex System
Research, The Beckman Institute, University of Illinois, Urbana.
[MAYER-KRESS 1993] MAYER-KRESS G., CHOI I., WEBER N., BARGAR R., HÜBLER
A. (1993) - Musical Signals from Chua's Circuit, Center for Complex
System Research, The Beckman Institute, University of Illinois, Urbana.
[MAYER-KRESS 1993] MAYER-KRESS G., CHOI I., BARGAR R. (1993) - Sound
Synthesis and Music Composition using Chua's Oscillator, Center for
Complex System Research, The Beckman Institute, University of Illinois,
Urbana.
[Mc ADAMS 1987)] Mc ADAMS S. et Bregman A. (1987)- L'audition des flux
musicaux, in Marsyas, Institut de pédagogie musicale et chorèographique,
La Villette, Paris (3-4) décembre 1987, PP 97-118.
[MESNAGE 1988] MESNAGE M., RIOTTE A., (1988) - Un modèle informatique
d'une pièce de STRAVINSKY, in Analyse Musicale, ndeg.10, Paris.
[NELSON 1994] NELSON G. L. (1994) - Real Time Transformation of Musical
Material with Fractal Algorithms, papier obtenu avec le compositeur,
fnelson@oberli.edu.
[PEITGEN 1993] PEITGEN H. O. , JÜRGENS Harmut, SAUPE Dietmar (1993)
- Chaos and Fractals, New Frontiers of Science, Springer-Verlag,
New York.
[QUETELET 1835] QUETELET A. (1835) - Sur l'homme et le développement
de ses facultés, dans HILLION A. (1986) Les Théories Mathématiques
des Populations , Que-Sais-Je?, P.U.F.., France.
[RIOTTE 1996] RIOTTE A., (1996) - Formes variables, quelques expériences,
in Simposium, Composition, Modélisation et Ordinateur, 12 et 13 avril
1996, IRCAM.
[WALLISER 1977] WALLISER Bernard (1977)- Systèles et Modèles,
Editions du Seuil, Paris.