4.5 Improvements of the Discrete Cepstrum Method

  
4.5.1 Regularization

The technique of regularization , developed in [GR90,COM97] improves the smoothness of the spectral envelope. Its idea is to penalize too steep a slope of the spectral envelope by adding a regularization term  $\lambda B$ to the matrix A, defined in equation (3.19), where B is a quadratic matrix of size p+1, the diagonal of which is defined by:

   $$b_{ii} = 8 \pi^2 (i - 1)^2.$$

Then the discrete cepstrum algorithm proceeds as in section 3.4.

 

tex2html_comment_mark>

The effect of regularization can be seen in figure 3.8. The disadvantage or regularization is that sometimes a steep slope is necessary to reach a single extremely situated peak, as with the low peak at about 3400 Hz in the figure. With regularization, the curve falls short of reaching it.

  
4.5.2 Stochastic Smoothing (The Cloud Method)

The cloud  method developed by Thierry Galas and Xavier Rodet in [GR90] is a way to get a smoother spectral envelope with the discrete cepstrum algorithm. The method generates a cloud of points around each partial on the frequency-amplitude plane to give the discrete cepstrum algorithm more freedom trying to fit a curve that links all the partials.

  

Figure 3.9: The cloud of points around the original partial generated by stochastic smoothing with indifferent slope (left), and with a hint for a rising slope (right)

The added points x_1..4 are displaced from the original point x₀ at frequency f₀ and amplitude a₀ by a frequency shift fand an amplitude factor a as shown in figure 3.9 left:

$$x_1 = (f_0- f, \ a_0\makebox[\xml][c]{$\:\*\:$ } a)$$ (4.1)

$$x_2 = (f_0- f, \ a_0\makebox[\xml][c]{$\:/\:$ } a)$$ (4.2)

$$x_3 = (f_0+ f, \ a_0\makebox[\xml][c]{$\:\*\:$ } a)$$ (4.3)

$$x_4 = (f_0+ f, \ a_0\makebox[\xml][c]{$\:/\:$ } a)$$ (4.4)

Furthermore, the shape of cloud can be used to influence the behaviour of the spectral envelope, if additional information is known, as shown in figure 3.9 right. For example, with a configuration as in the figure, if it was known that a point is situated in the rising slope of a formant, the spectral envelope could be influenced to also prefer a rising slope. The displacement of the added points is given by

$$x_1 = (f_0- f_2, \ a_0\makebox[\xml][c]{$\:\*\:$ } a_2)$$ (4.5)

$$x_2 = (f_0- f_1, \ a_0\makebox[\xml][c]{$\:/\:$ } a_1)$$ (4.6)

$$x_3 = (f_0+ f_1, \ a_0\makebox[\xml][c]{$\:\*\:$ } a_1)$$ (4.7)

$$x_4 = (f_0+ f_2, \ a_0\makebox[\xml][c]{$\:/\:$ } a_2)$$ (4.8)

However, to avoid too strong a deviation of the spectral envelope from the original point, weighting  is introduced in the discrete cepstrum algorithm to attenuate the influence of the added points with respect to the original point. The original point is weighted with a factor of 5, whereas the added points are weighted with a factor of 1, as expressed by the thickness of the points in figure 3.9. The weighting h_i is introduced in the calculation of the error criterion in equation (3.17):

$$E = \sum_{i=1}^n {h_i \left( \log s_i P(\omega_i) - \log x_i \right)^2}$$

Thus, equation (3.19) will become

$$a_{ij} = \sum_{k=1}^n {h_i \ \cos \omega_k i \ \cos \omega_k j}$$

and equation (3.21) is changed to

$$b_i = \sum_{k=1}^n {h_i \log \frac{x_k}{s_k} \cos \omega_k i}$$

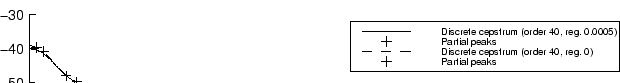
From a more formal point of view, the cloud method is in fact a replacement of each original partial (spectral peak) $(\omega_i, x_i)$by a probability distribution $\pi_i (\omega, x)$. This is due to the impossibility of knowing the precise position of the spectral peaks, which is reflected by the probability distribution, while before a perfect knowledge of the spectral peaks was assumed.

The new error criterion, assuming s_i = h_i = 1, is:

$$E = \sum_{i=1}^n {\int \!\!\! \int \pi_i (\omega, x) \left(... ...\omega_i) - \log x_i \right)^2 \mathrm d \omega \mathrm d x}$$

The distribution $\pi_i$ can be sampled, i.e. each spectral peak $(\omega_i, x_i)$ is replaced by a set of peaks $(\omega_k, x_k)$, to yield the cloud of points described at the beginning of this section. Formally, for a gaussian distribution

$$\pi_i (\omega, x) = e^{-\alpha^2 (x-x_i)^2} e^{-\beta^2 (\omega-\omega_i)^2}$$

the weights would then be $h_k = \pi (\omega_k, x_k)$.

 

tex2html_comment_mark>

Figure 3.10 shows the improvement of discrete cepstrum spectral envelope estimation with stochastic smoothing. The cloud method can also be combined with regularization, described in section 3.5.1 to further improve results.

  
4.5.3 Logarithmic Frequency Scaling

As we have seen in section 3.4, the discrete cepstrum algorithm is of cubic complexity in p, the order of the discrete cepstrum. This means that we must try to reduce the order necessary for a good estimation of the spectral envelope, to keep computation times short. One way to achieve this is to judiciously spend the preciseness or resolution where it is most needed, and reduce it where it is not so important. We can exploit the properties of the human auditory system, for that matter.

Due to the logarithmic frequency resolution of the human hearing, which also led to the mel frequency scale , we don't need to be very exact with the spectral envelope in higher frequency ranges. It suffices to represent the rough location of energy, whereas in the low frequencies, very slight deviations in frequency and amplitude are perceptible. Therefore we can introduce a logarithmic frequency scaling  similar to the mel scale, as suggested in [GR91b], which is linear below a given break frequency , and logarithmic above. The mel scale is defined by

$$\textrm{mel} (f) = \left\{\begin{array}{ll} f \* \frac{f_m... ...\frac{f}{f_b}) & \textrm{if} \quad f > f_b \end{array}\right.$$

where f_b is the break frequency and f_m is the mel frequency at the break point.

Taking this formula directly poses problems, because frequencies can surpass the Nyquist frequency f_s / 2, which is to be avoided, because it disturbs the validity of the subsequent calculations. Normalizing the range of the mel function to within the Nyquist frequency yields:

$$\textrm{melnorm} (f) = \left\{\begin{array}{ll} \frac {f}{... ...}{f_b}) \* f_n & \textrm{if} \quad f > f_b \end{array}\right.$$

where f_n is the normalization factor given by

$$f_n = \frac {\frac{1}{2} f_s} {1 + \log_{10} \frac{\frac{1}{2} f_s}{f_b}}$$

The new logarithmic scaling function melnorm no longer depends on f_m.

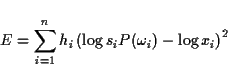
The effect of logarithmic frequency scaling can be seen in figure 3.11.

 

tex2html_comment_mark>

As an additional advantage, spectral envelopes stored with a logarithmic frequency support take less space. Also the complexity of synthesis can be reduced when there are fewer points needed to represent a spectral envelope.

To retrieve the spectral envelope from cepstral coefficients obtained with logarithmic frequency scaling, the frequencies f_i of the bins of the envelope (see end of section 3.3) have to be converted to logarithmic scale:

f'_i = melnorm (f_i)

Then proceed with equations (3.9) and (3.10).

There is one pitfall in the application of logarithmic frequency scaling: Performing the linear-to-logarithmic transformation before applying the cloud deteriorates the results slightly. To see why this is so, remember that the cloud algorithm (section 3.5.2) adds points with a constant linear shift around each peak frequency, which will subsequently be stretched for the linear part or unsymmetrically converted to the logarithmic scale for the rest.

   
4.5.4 Adding Points to Control the Envelope

There are two situations where the behaviour of the discrete cepstrum spectral envelope has to be controlled by adding artificial points to the partials for discrete cepstrum estimation: at the borders and between the highest partial and the upper border. If the cloud method of stochastic smoothing (section 3.5.2) is selected, these points would be added before the cloud is applied (i.e. each added point will have a cloud of points around it).

 

tex2html_comment_mark>

The border points  are added at the frequencies m and at (f_s/2 - m) with half the amplitude of the lowest/highest partial, respectively. This will force the spectral envelope to have a downward slope at the borders. Thus, if--by downward transposition of the partials while keeping the spectral envelope--there is a partial which is moved to lower frequencies, there is no risk that it will suddenly rise in amplitude, but it will be faded out smoothly. Figure 3.12 shows the effect of adding border points.

However, if the frequency of the lowest partial is less than m, the low border point is not added, since this would obviously cause an unjustified dip in the spectral envelope, which would disturb the smoothness. We don't have to worry about the border condition then anyway, since then the lowest partial would be very close to the 0 Hz border, constraining the spectral envelope enough to prevent it from rising. The same holds analogously for the high border point.

The filling points  fill up a possible gap between the frequency of the highest partial and f_s/2 with very low amplitude peaks, spaced at f_s / 2n (n being the number of points of the envelope requested). This is to avoid too much freedom for the spectral envelope. If the spectral envelope was unconstrained in a large frequency range, it would oscillate wildly.