6.1 Interpolation

First of all it must be noted that there are two different meanings of the word interpolation. One meaning refers to finding a value of a function that is given only at discrete points, when the value is inbetween two of the given points. With spectral envelopes, we use interpolation in this sense when we want to know the value of the envelope v(f) at an arbitrary frequency f, which is not one of the given points of the envelope. 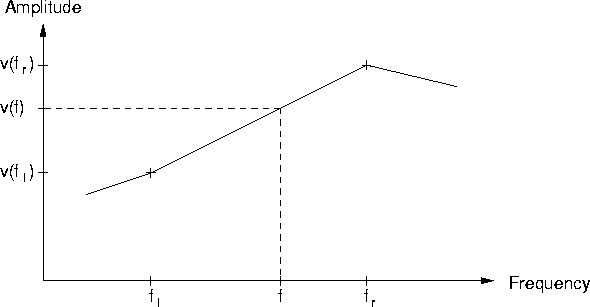^6.1 If f_l and f_r are the two points closest to f, then the linear interpolation  is:

   $$v(f) = \frac{v(f_r) - v(f_l)}{f_r - f_l} (f - f_l) + v(f_l)$$

which is the value of v(f) if the given points of the envelope are considered to be connected by line segments (see figure 5.3).

  

Figure 5.3: Linear interpolation within a spectral envelope

   
6.1.1 Interpolation between Spectral Envelopes

The second meaning of interpolation is finding an intermediate state in the gradual transition from one parameter set to another, in our case going from one spectral envelope to another. This interpolation between envelopes  is in fact a weighted sum  of the spectral envelopes. It can always be reduced to the first sense of interpolation, in that we take the linearly interpolated values v₁(f) and v₂(f) for each frequency f of two spectral envelopes and interpolate between them by an interpolation factor  m. If m=0 we will keep the original spectral envelope v₁, if m=1 we will receive the target spectral envelope v₂:

  v_m(f) = (1 - m) v₁(f) + m v₂(f)

If we consider that the envelopes can be sampled each at a different set of discrete frequency points f₁ and f₂, to actually compute the interpolated spectral envelope we have to build the union of the frequency points $f_u = f_1 \cup f_2$ and compute the interpolated value at each point of f_u.

   
6.1.2 Shifting Formants

When dealing with the spectral envelope of speech or the singing voice, we want to respect the formant structure of the envelope. This means that if we want to interpolate between two spectral envelopes, we don't want the amplitudes at each frequency interpolated as in equation (5.2), but shift the formants from their place in the original spectral envelope to that in the target spectral envelope. In fact, we want to simulate the effect of interpolating the articulatory parameters of the vocal tract. Figure 5.4 explains the different approaches.

  

Figure 5.4: Formant interpolation  versus formant shift : The upper row shows two spectral envelopes whose single formants are to be interpolated. In the lower left figure we see what we get from the direct interpolation of spectral envelopes--which is a weighted sum of the two curves, here with an interpolation factor of 0.5. The original formants are shown as dashed curves. The lower right figure shows what we really want: interpolating the parameters of the formants, resulting in a frequency shift.

The prerequisites for shifting formants in this way are of course that we know where the formants are located, and which formant in the original spectral envelope is associated with which formant in the target spectral envelope. The former is not at all obvious and is a question of formant detection . The latter is even more difficult for an automated method without providing manual input. It is a question of labeling the formants of successive time frames to generate formant tracks.

Fortunately, for some applications, we know a priori where the formants should be. For example, when treating the voice in a piece where the lyrics are known, like an opera. Then it is known which vowels are sung, and thus we can look up the formant positions in the formant tables from phonetics literature. In this case, the spectral envelope representation would be augmented by fuzzy formants, or a spectral envelope representation using exact formants will be provided, as described in section 4.5.

   
6.1.3 Shifting Fuzzy Formants

The fuzzy formant representation of spectral envelope consists of an envelope in spectral representation plus several formant regions with an index for identification. Given two spectral envelopes with two fuzzy formants with the same index, it is still not clear how the intermediate spectral envelopes, with the formant on its way from its position in the original envelope to that in the target envelope, are to be generated. Several questions arise: How to fill the hole the formant leaves when it starts to move away? What to do with the envelope in the places the formant moves over? How should the shape of the formant change between the original and the target shapes?

After an idea by Miller Puckette, it is possible to interpolate an envelope in spectral representation in a way that formants are shifted exactly as we want. The idea is to first integrate over the envelopes (in the discrete case, this amounts to building the cumulative sum of the spectral envelope), and then to horizontally interpolate  between the integrals. We retrieve the interpolated formant by subsequent differentiation of the result.

  

Figure 5.5: Interpolation of formants by horizontal interpolation of the integral. All amplitudes are normalized. The upper row shows the integrals (the cumulative sum) of the two formants shown as dashed spectral envelopes. The lower left figure shows the horizontal linear interpolation by a factor of 0.5 of the interpolated integrals, drawn again as dashed lines. Taking the derivative of the result in the lower right figure reveals the almost perfectly shifted formant. (The original formants are shown again in dashed lines for clarity.)

That the idea works can be seen in figure 5.5. Formally, the method can be described like this: Starting from two spectral envelopes v₁(f) and v₂(f), considered as continuous functions over $0 \le f \le f_s/2$, we construct the cumulative integral functions V₁(F) and V₂(F), and normalize:

$$V_i (F) = \frac{1}{s_i} \int_0^{F} \!\!\! v_i \: \mathrm d f \qquad \textrm{for\ } i=1,2$$

With

$$s_i = \int_0^\frac{f_s}{2} \!\! v_i \: \mathrm d f$$

being the maximum values of V_i(F). Then we invert these functions

$$V_i (F) = A \iff V_i^{-1} (A) = F \qquad \textrm{for\ } i=1,2 \textrm{\ and\ } 0 \le A \le 1$$

and interpolate by weighted sum with an interpolation factor m to receive $\bar{V}^{-1}(A)$:

$$\bar{V}^{-1} (A) = (1 - m) V_1^{-1} (A) + m V_2^{-1} (A)$$

After inverting $\bar{V}^{-1}(A)$ back to normal coordinates

$$\bar{V}^{-1} (A) = F \iff \bar{V} (F) = A$$

we differentiate to retrieve the interpolated spectral envelope $\bar{v}(f)$:

$$\bar{v}(f) = \frac{\mathrm d \bar{V}}{\mathrm d f}$$

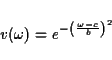
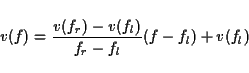
Unfortunately, this works only for one formant to be interpolated, as can be seen in figure 5.6. Nevertheless, we can do better if we have the information of formant regions, i.e. we know where the two formants to be interpolated lie in their respective spectral envelopes. In this case, we can restrict the technique of horizontal interpolation of the integral to the given formant regions, with an appropriate fade-in and fade-out of the region borders.

  

Figure 5.6: Interpolation of two formants by horizontal interpolation of the integral. Obviously, the result in the lower right graph does not correspond to the interpolation of the formant parameters.

6.1.4 Interpolation between Precise Formants

If both of the two spectral envelopes to be interpolated are given as precise formants with their index i, center frequency f_i, amplitude a_i, and bandwidth b_i as parameters, interpolation becomes trivial. Simply the formant parameters need to be linearly interpolated, using equation (5.1) accordingly.

   
6.1.5 Summary of Formant Interpolation

Summing up the different possibilities of interpolation of spectral envelopes, we can recognize a hierarchy in the spectral envelope representations in regard of formant interpolation. The hierarchy is, from highest to lowest:

1.

Precise formants: can be interpolated perfectly

2.

Fuzzy formants: can be interpolated reasonably well

3.

Spectral representation of envelopes: can not be interpolated respecting formants

With each step down we lose some information necessary for formant interpolation. We can convert downwards step by step:

1.

$\rightarrow$ 2. Convert precise formants to fuzzy formants by evaluating the spectral envelope given by the precise formants after equation (4.1), and storing it in spectral representation, while calculating the formant regions from the precise formant parameters.

2.

$\rightarrow$ 3. Convert fuzzy formants to spectral representation by simply discarding the formant regions.

We cannot, however, convert upwards, because that would mean adding information (by simple calculations, that is--of course, methods to detect formant shapes in spectral envelopes exist, but these are the subject of a field of research of its own.)

This means that, when spectral envelopes in different representations have to be interpolated, we can't do better than going down to that representation of the two which is lowest in level, discarding the formant information of the higher one.