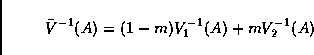6.3 Other Manipulations

The manipulations not covered by the preceding sections concern mainly manipulations of the frequency location of parts of a spectral envelope. One possibility I named skewing  is to selectively displace a part of the spectral envelope in frequency. In order to avoid holes, the amount of displacement (the frequency shift ) is faded in and out by a skew-function, as in figure 5.7.

  

Figure 5.7: The left figure shows the linear skew function, determining the frequency shift dependent on frequency, while to the right, a smoother gaussian skewing function is shown.

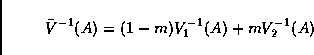Four parameters specify the skewing: The lower and upper frequencies l and u determine the range of the spectral envelope to be affected. The middle frequency m will be moved to the new frequency n, while the spectral envelope left and right from m will be shifted gradually less the further the distance to m. The result of skewing with a linear skew function is shown in figure 5.8. Many other skew functions and more parameters are possible.

 

tex2html_comment_mark>

Other possible frequency manipulations  are a shift of the whole spectral envelope v, as well as compression  or dilatation  by a transposition  factor t:

$$v_{transp} (f) = v(\frac{f}{t}) \qquad \textrm{for all\ } 0 \le f \le f_s/2$$