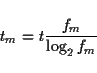



Next: 8. Implementation
Up: 7. Sound Synthesis with
Previous: 7.1 Additive Synthesis
7.2 Filtering
If the sound to be changed is not represented by partials but comes as
a time-domain signal, the modulating spectral envelope has to be converted to a
filter that is to be applied to the signal. There are always two
possibilities how to actually carry out the filtering:
How to calculate either one of the forms of the filter will be
described in the following, for each possible representation of the
spectral envelope.
- Spectral representation
-
If the spectral envelope is in canonical representation directly as a curve in the
frequency-amplitude domain, the frequency-domain filter is given
straightforward by the evaluation of the spectral envelope v(f) at the
frequencies fi, which are the frequency bins used for filtering::
H(fi) = v(fi)
The time-domain filter is the inverse Fourier transform of the
frequency-domain filter:
This time-domain filter will in general be more costly to apply than a
time-domain filter derived from filter coefficients as shown below,
since the impulse response can be as long as the number of bins in
H.
- Cepstral coefficients
-
If the spectral envelope is represented as cepstral coefficients ci, for
frequency-domain filtering, we have to reconstruct the spectral envelope, which
defines the transfer function of H, by inversing the operations
carried out in cepstrum estimation (section 3.3):
H = exp(F-1 (ci))
Which is equivalent to an evaluation of this formula at the desired
frequency bins 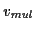 :7.1
:7.1
For time-domain filtering, the impulse response h is computed by the
inverse Fourier transform of the transfer function H:
h = F-1(H) = F-1(exp(F-1 (ci)))
- LPC-coefficients
-
The predictor coefficients
ai, i=1..p are well suited to
frequency-domain filtering. They describe the analysis filter A,
which is inverse of the transfer function H, corrected by a gain
factor g:
The time-domain filter could be derived as usual by equation (6.6),
however, it follows from the properties of LPC-estimation
(section 3.2) that we can use the predictor coefficients directly:
What's more, by using the reflection coefficients ki, we can apply
the much more efficient filter structure of a lattice filter , and can implement the filter directly as shown in figure 6.2.





Next: 8. Implementation
Up: 7. Sound Synthesis with
Previous: 7.1 Additive Synthesis
Diemo Schwarz
1998-09-07