next up previous contents index
Next: 8.5 The Spectral Envelope Up: 8. Implementation Previous: 8.3 General Considerations for

Subsections

    
8.4 The Development of the Spectral Envelope Library

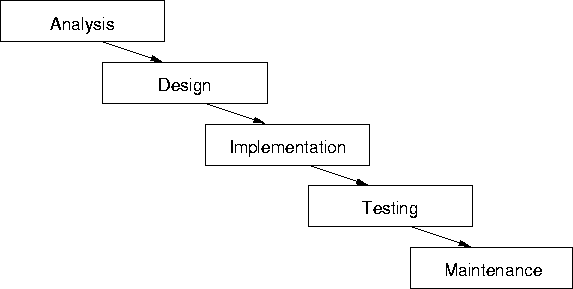
This section describes how the spectral envelope library was developed. First, the architecture will be described as the central design documentation in 7.4.1. Then, a few words will be said about how we got there from analysis, and some more words about how we're going from there to implementation in 7.4.2.

   
8.4.1 The Architecture

The architecture of the spectral envelope library is described using the notation introduced in section 7.2. The top-level data flow diagram in figure 7.7 shows the different transformations between sound data and the spectral envelope representation. Subsequently, the data and functional classes will be further decomposed into subclasses. An additional data class Control Data, which provides input to every functional class, is left out for the sake of lisibility.


  
Figure 7.7: Top level data flow diagram of the base classes of the spectral envelope library. The base classes will be refined in the subsequent diagrams.
\begin{figure}\centerline{\epsfbox{pics/dfd-toplevel.eps}} \end{figure}

The two main data classes, Sound Data and Spectral Envelope, the representation class, and their subclasses are shown in figures 7.8 and 7.9, respectively.


  
Figure 7.8: The Sound Data class, and its different subclasses, with the transformations between them
\begin{figure}\centerline{\epsfbox{pics/dfd-data.eps}} \end{figure}


  
Figure 7.9: The representation data class Spectral Envelope and its subclasses, the different representations of spectral envelopes. The Conversion functional class does all conversions from one spectral envelope representation in another and is not further refined.
\begin{figure}\centerline{\epsfbox{pics/dfd-representation.eps}} \end{figure}

The diagrams in figures 7.10 to 7.15 show the functional classes Estimation, Synthesis, and Interpolation. They are grouped in pairs of two. The first diagram of each pair shows the subclasses of the respective functional class. The second diagram of each pair shows the input and output data flows of the subclasses. (The data flows of the base classes are all shown in the top-level diagram in figure 7.7.)


  
Figure 7.10: The Estimation class and its subclasses, the implemented methods for spectral envelope estimation
\begin{figure}\centerline{\epsfbox{pics/dfd-estimation.eps}} \end{figure}


  
Figure 7.11: The subclasses of the Estimation functional class with their Sound Data input data flows and Spectral Envelope output data flows.
\begin{figure}\centerline{\epsfbox{pics/dfd-estimation-flow.eps}} \end{figure}


  
Figure 7.12: The Synthesis functional class and its subclasses, the different methods for synthesis with spectral envelopes
\begin{figure}\centerline{\epsfbox{pics/dfd-synthesis.eps}} \end{figure}


  
Figure 7.13: The subclasses of the Synthesis functional class with their input/output data classes (the subclasses of Sound Data and a spectral envelope as the data class Spectral Envelope)
\begin{figure}\centerline{\epsfbox{pics/dfd-synthesis-flow.eps}} \end{figure}


  
Figure 7.14: The Interpolation functional class and its subclasses, the methods for interpolation of spectral envelopes. Formant Interpolation is a separate base class because the matching of formant indices is handled there.
\begin{figure}\centerline{\epsfbox{pics/dfd-interpolation.eps}} \end{figure}


  
Figure 7.15: The subclasses of the Interpolation functional class with their input/output data classes (the subclasses of Spectral Envelope). As can be seen, conversion can only be done in the direction to the less structured representation.
\begin{figure}\centerline{\epsfbox{pics/dfd-interpolation-flow.eps}} \end{figure}


  
Figure: The class and its subclasses, the spectral envelopes
\begin{figure}\centerline{\epsfbox{pics/dfd-.eps}} \end{figure}

   
8.4.2 Going from Analysis to Implementation

The architecture diagrams in figures 7.7 to 7.15 specify the design of the spectral envelope library. However, they are directly derived from the analysis of the requirements for the library. In fact, the diagrams that are the output of the analysis phase (the requirements engineering) look the same, except that some details like usage-relationships are missing. This is the reason that the analysis phase is not explicitly documented. This supports the claim, by the way, that the adapted notation is indeed useful, because it offers a transparent transition from the analysis of the software system to its design.

In going from design to implementation, however, it is impossible to make a transparent transition, since there we reach the boundary of the object-oriented paradigm . While in analysis and design, it was still possible to describe the world as consisting of interacting objects, each pertaining to one of several classes, in our implementation in non-object-oriented C, we have to talk about functions, modules, and data structures. Because we can't transfer the object-oriented paradigm  completely to implementation, some desirable properties of object-oriented programming  will not hold. Specifically, the aspects of encapsulation, inheritance and type-polymorphism will be lost, as explained in the following:

  
Encapsulation

The C-structures that will be used instead of classes offer no compiler-enforced protection mechanism regarding the access to the data fields. However, for the data classes explained below, access functions  can be provided, that set the value of one data field, or return its value. If the user of the library by convention uses these access functions, sufficient encapsulation between the interface and the implementation of the data structures is provided. This means that, for example in the case the internal data structures change, the code using these structures will not have to be changed.

For some data structures such as the one holding the estimation parameters, encapsulation is even undesirable, since

  
Inheritance

The inheritance relations (also called subtype  or generalization /specialization  relations) used in the analysis and design will not be visible in the implementation. Instead, the classes will be mapped to C-structures as shown in section 7.4.3.

In theory, it is always possible to replace inheritance by aggregation, i.e. the subclasses contain the base class, but for reasons explained below,

  
Polymorphism

Polymorphism  is closely linked to inheritance and means the access to a certain functionality that applies to all subclasses of a base class by one method name. This name maps to the appropriate method 8.3 of the actual subclass.

Polymorphism could be mimicked in C by storing pointers to member functions with each object. Apart from the complexity and usage of space of that procedure, type polymorphism is, on closer scrutiny, not really necessary for the spectral envelope library. This is because the number of generic functions (e.g. save) which have to be applied to all subtypes of one general type are fairly few. Instead, specialized functions for the classes exist. For example, the three different subclasses of sound data (Signal, Spectrum, Partials) are processed by three different estimation methods (LPC Analysis, Cepstrum, Discrete Cepstrum) to yield two different output data types (LPC Coefficients, Cepstral Coefficients). I.e. the data flows on parallel ``tracks'' that rarely cross. In another case, formant interpolation, it is necessary to know the actual subtype of spectral envelope representation (Sampled Spectral Envelope, Precise Formants, Fuzzy Formants) to choose the specialized method to perform the formant shift (see section 5.1.2). Therefore, it is advantageous to keep the subtype information explicit in the code and not generalize to a superclass.

   
8.4.3 Example of a Data Structure: The Spectral Envelope Class

As an example of the implementation of the data classes, the definition of the structures for the Spectral Envelope class, from the class diagram in figure 7.9, are given below:

The sampled spectral envelope, or spectral representation, is: 

typedef struct 
{
    float       maxfreq;     /* upper border of env (maxfreq = sampling rate/2) */
    int         numenv;      /* number of points in envelope                    */
    float       *env;        /* numenv spectral envelope amplitude values       */
      
    float       fstep;       /* size of bin in env  (fstep = sr / numenv)       */
    seScale     scale;       /* frequency scale for storage                     */
    float       breakfreq;   /* break frequency for log scale                   */
}   seSpecEnv;

Where seScale gives the type of the scaling and is defined as: 

typedef enum { seScLinear, seScLog, seScNum }   seScale;

For the spectral envelope representation as precise formants, we use a list of structures for formants, and a residual spectral envelope, which represents all components that are not of the shape of a formant: 

typedef struct 
{
    float       centerfreq;     /* precise formant parameters */
    float       amplitude;
    float       bandwidth;
}   seFormant;


typedef struct 
{
    int         numformants;    /* number of precise formants   */
    seFormant   *formants;      /* numformants precise formants */
    seSpecEnv   residual;       /* residual spectral envelope   */
}   sePreciseFormants;

For the fuzzy formant representation, we use a list of formant regions within a sampled spectral envelope: 

typedef struct 
{
    float       lower;          /* region boundary frequencies (Hz) */
    float       center;
    float       upper;
    float       salience;       /* how sure we are it is a formant  */
}   seRegion;


typedef struct 
{
    int         numformants;    /* number of precise formants   */
    seRegion    *formants;      /* numformants precise formants */
    seSpecEnv   specenv;        /* spectral envelope            */
}   sePreciseFormants;

next up previous contents index
Next: 8.5 The Spectral Envelope Up: 8. Implementation Previous: 8.3 General Considerations for
Diemo Schwarz
1998-09-07