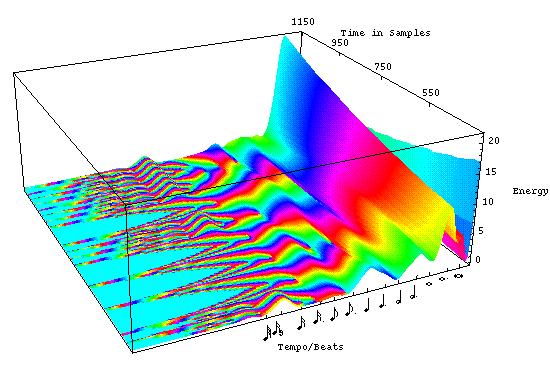
A "Rhythmic Contour Map" combining magnitude and phase outputs from the continuous wavelet analysis of a portion of the snare drum rhythm of Maurice Ravel's "Bolero".
Evaluation of a Multiresolution Model of Musical Rhythm Expectancy on Expressive Performances
Leigh M. Smith
(PDF, 1 page poster presentation, Programme for 12th Rhythm Perception and Production Workshop, Lille, France 2009)
A computational multi-resolution model of musical rhythm expectation has been recently proposed based on cumulative evidence of rhythmic time-frequency ridges (Smith & Honing 2008a). This model was shown to demonstrate the emergence of musical meter from a bottom-up data processing model, thus clarifying the role of top-down expectation. Such a multiresolution time-frequency model of rhythm has also been previously demonstrated to track musical rubato well, with both synthesised (Smith & Honing 2008b) and performed audio examples (Coath et. al 2009). The model is evaluated for it's capability to generate accurate expectation from human musical performances. The musical performances consist of 63 monophonic rhythms from MIDI keyboard performances, and 50 audio recordings of popular music. The model generates expectations as forward predictions of times of future notes, a confidence weighting of the expectation, and a precision region. Evaluation consisted of generating successive expectations from an expanding fragment of the rhythm. In the case of the monophonic MIDI rhythms, these expectations were then scored by comparison against the onset times of notes actually then performed. The evaluation is repeated across each rhythm. In the case of the audio recording data, where beat annotations exist, but individual note onsets are not annotated, forward expectation is measured against the beat period. Scores were computed using information retrieval measures of precision, recall and F-score (van Rijsbergen 1979) for each performance. Preliminary results show mean PRF scores of (0.297, 0.370, 0.326) for the MIDI performances, indicating performance well above chance (0.177, 0.219, 0.195), but well below perfection. A model of expectation of musical rhythm has been shown to be computable. This can be used as a measure of rhythmic complexity, by measuring the degree of contradiction to expectation. As such, a rhythmic complexity measure is then applicable in models of rhythmic similarity used in music information retrieval applications.
Model Cortical Responses For The Detection Of Perceptual Onsets And Beat Tracking In Singing
Martin Coath, Susan Denham, Leigh M. Smith, Henkjan Honing, Amaury Hazan, Piotr Holonowicz, Hendrik Purwins
(PDF, 12 pages, in Connection Science, 21(2 & 3), 2009 pages 193-205)We describe a biophysically motivated model of auditory salience based on a model of cortical responses and present results that show that the derived measure of salience can be used to identify the position of perceptual onsets in a musical stimulus successfully. The salience measure is also shown to be useful to track beats and predict rhythmic structure in the stimulus on the basis of its periodicity patterns. We evaluate the method using a corpus of unaccompanied freely sung stimuli and show that the method performs well, in some cases better than state-of-the-art algorithms. These results deserve attention because they are derived from a general model of auditory processing and not an arbitrary model achieving best performance in onset detection or beat-tracking tasks.
A Multiresolution Model of Rhythmic Expectancy
Leigh M. Smith and Henkjan Honing
(PDF, 6 pages, in Proceedings of the Tenth International Conference on Music Perception and Cognition pages 360-365, Sapporo, Japan, 2008)
We describe a computational model of rhythmic cognition that predicts expected onset times. A dynamic representation of musical rhythm, the multiresolution analysis using the continuous wavelet transform is used. This representation decomposes the temporal structure of a musical rhythm into time varying frequency components in the rhythmic frequency range (sample rate of 200Hz). Both expressive timing and temporal structure (score times) contribute in an integrated fashion to determine the temporal expectancies. Future expected times are computed using peaks in the accumulation of time-frequency ridges. This accumulation at the edge of the analysed time window forms a dynamic expectancy. We evaluate this model using data sets of expressively timed (or performed) and generated musical rhythms, by its ability to produce expectancy profiles which correspond to metrical profiles. The results show that rhythms of two different meters are able to be distinguished. Such a representation indicates that a bottom-up, data-oriented process (or a non-cognitive model) is able to reveal durations which match metrical structure from realistic musical examples. This then helps to clarify the role of schematic expectancy (top-down) and it's contribution to the formation of musical expectation.
Time-Frequency Representation of Musical Rhythm by Continuous Wavelets
Leigh M. Smith and Henkjan Honing
(PDF, 25 pages, in Journal of Mathematics and Music, 2(2), 2008 pages 81-97)
A method is described that exhaustively represents the periodicities created by a musical rhythm. The continuous wavelet transform is used to decompose an interval representation of a musical rhythm into a hierarchy of short-term frequencies. This reveals the temporal relationships between events over multiple time-scales, including metrical structure and expressive timing. The analytical method is demonstrated on a number of typical rhythmic examples. It is shown to make explicit periodicities in musical rhythm that correspond to cognitively salient “rhythmic strata” such as the tactus. Rubato, including accelerations and retards, are represented as temporal modulations of single rhythmic figures, instead of timing noise. These time varying frequency components are termed ridges in the time-frequency plane. The continuous wavelet transform is a general invertible transform and does not exclusively represent rhythmic signals alone. This clarifies the distinction between what perceptual mechanisms a pulse tracker must model, compared to what information any pulse induction process is capable of revealing directly from the signal representation of the rhythm. A pulse tracker is consequently modelled as a selection process, choosing the most salient time-frequency ridges to use as the tactus. This set of selected ridges are then used to compute an accompaniment rhythm by inverting the wavelet transform of a modified magnitude and original phase back to the time domain.
Evaluation Of Multiresolution Representations Of Musical Rhythm
Leigh M. Smith and Henkjan Honing
(PDF, 4 pages, in Proceedings of the International Conference on Music Communication Science, Sydney, 2007)
A dynamic representation of musical rhythm, the multiresolution analysis using the continuous wavelet transform (CWT), is evaluated using a dataset of the interonset intervals of 105 national anthem rhythms. This representation decomposes the temporal structure of a musical rhythm into time varying frequency components in the rhythmic frequency range (sample rate of 200Hz). Evidence is presented that the beat (typically quarter-note or crochet) and the bar (measure) durations of each rhythm are revealed by this transform. Such evidence suggests that the pattern of time intervals, when analyzed with the CWT, function as features that are used in the process of forming a metrical interpretation. Since the CWT is an invertible transform of the interonset intervals in each rhythm, this result is interpreted as setting a minimum capability of discrimination that any perceptual model of beat or meter can achieve. It indicates that a bottom-up, data-oriented process (or a non-cognitive model) is able to reveal durations which match metrical structure from realistic musical examples. This then characterises the data and behaviour of a top-down cognitive model which must interact with the bottom-up process.
Evaluating and Extending Computational Models of Rhythmic Syncopation in Music
Leigh M. Smith and Henkjan Honing
(PDF, 4 pages, in Proceedings of the 2006 International Computer Music Conference, New Orleans, pages 688-91)
What makes a rhythm interesting, or even exciting to listeners? While in the literature a wide range of definitions of syncopation exists, few allow for a precise formalization. An exception is Longuet-Higgins and Lee (1984), that proposes a formal definition of syncopation. Interestingly, this model has never been challenged or empirically validated. In this paper the predictions made by this model, along with alternative definitions of metric salience, are compared to existing empirical data consisting of listener ratings on rhythmic complexity. While correlated, noticable outliers suggest processes in addition to syncopation contribute to listeners judgements of complexity.
Next Steps from NeXTSTEP: MusicKit and SoundKit in a New World
Stephen Brandon and Leigh M. Smith
(PDF, 4 pages, in Proceedings of the 2000 International Computer Music Conference, Berlin, pages 503-506)
This paper describes the new implementation and port of the NeXT MusicKit, and a clone of the NeXT SoundKit - the SndKit, on a number of different platforms, old and new. It will then outline some of the strengths and uses of the kits, and demonstrate several applications which have made the transition from NeXTSTEP to MacOS-X and WebObjects/NT.
A Multiresolution Time-Frequency Analysis and Interpretation of
Musical Rhythm
Leigh M. Smith
(PDF, 191 pages, UWA PhD Thesis, October 2000, Department of Computer Science, University of Western Australia)
Computational approaches to music have considerable problems in representing musical time. In particular, in representing structure over time spans longer than short motives. The new approach investigated here is to represent rhythm in terms of frequencies of events, explicitly representing the multiple time scales as spectral components of a rhythmic signal.
Approaches to multiresolution analysis are then reviewed. In comparison to Fourier theory, the theory behind wavelet transform analysis is described. Wavelet analysis can be used to decompose a time dependent signal onto basis functions which represent time-frequency components. The use of Morlet and Grossmann's wavelets produces the best simultaneous localisation in both time and frequency domains. These have the property of making explicit all characteristic frequency changes over time inherent in the signal.
An approach of considering and representing a musical rhythm in signal processing terms is then presented. This casts a musician's performance in terms of a conceived rhythmic signal. The actual rhythm performed is then a sampling of that complex signal, which listeners can reconstruct using temporal predictive strategies which are aided by familarity with the music or musical style by enculturation. The rhythmic signal is seen in terms of amplitude and frequency modulation, which can characterise forms of accents used by a musician.
Once the rhythm is reconsidered in terms of a signal, the application of wavelets in analysing examples of rhythm is then reported. Example rhythms exhibiting duration, agogic and intensity accents, accelerando and rallentando, rubato and grouping are analysed with Morlet wavelets. Wavelet analysis reveals short term periodic components within the rhythms that arise. The use of Morlet wavelets produces a "pure" theoretical decomposition. The degree to which this can be related to a human listener's perception of temporal levels is then considered.
The multiresolution analysis results are then applied to the well-known problem of foot-tapping to a performed rhythm. Using a correlation of frequency modulation ridges extracted using stationary phase, modulus maxima, dilation scale derivatives and local phase congruency, the tactus rate of the performed rhythm is identified, and from that, a new foot-tap rhythm is synthesised. This approach accounts for expressive timing and is demonstrated on rhythms exhibiting asymmetrical rubato and grouping. The accuracy of this approach is presented and assessed.
From these investigations, I argue the value of representing rhythm into time-frequency components. This is the explication of the notion of temporal levels (strata) and the ability to use analytical tools such as wavelets to produce formal measures of performed rhythms which match concepts from musicology and music cognition. This approach then forms the basis for further research in cognitive models of rhythm based on interpretation of the time-frequency components.
Modelling Rhythm Perception by Continuous Time-Frequency Analysis
Leigh M. Smith
(PDF, 4 pages, in Proceedings of the 1996 International Computer Music Conference, Hong Kong, pages 392-5)
The use of linear phase Gabor transform wavelets is demonstrated as a robust analysis technique capable of making explicit many elements of human rhythm perception behaviour. Transforms over a continuous time-frequency plane (the scalogram) spanning rhythmic frequencies (0.1 to 100Hz) capture the multiple periodicities implied by beats at different temporal relationships. Wavelets represent well the transient nature of these rhythmic frequencies in performed music, in particular those implied by agogic accent, and at longer time-scales, by rubato.
The use of the scalogram phase information provides a new approach to the analysis of rhythm. Measures of phase congruence over a range of frequencies are shown to be useful in highlighting transient rhythms and temporal accents. The performance of the wavelet transform is demonstrated on examples of performed monophonic percussive rhythms possessing intensity accents and rubato. The transform results indicate the location of such accents and from these, the inducement of phrase structures.
A Continuous Time-Frequency Approach To Representing Rhythmic Strata
Leigh M. Smith and Peter Kovesi
(PDF, 6 pages, in
Proceedings of the Fourth International Conference on Music
Perception and Cognition, Montreal 1996, pages 197-202).
Note that the printed
proceedings don't reproduce the greyscale images properly, so download
and print this version in preference to the proceedings version.
Existing theories of musical rhythm have argued for a conceptualization of a temporal hierarchy of rhythmic strata. This paper describes a computational approach to representing the formation of rhythmic strata. The use of Gabor transform wavelets (as described by Morlet and co-workers) is demonstrated as an analysis technique capable of explicating elements of rhythm cognition. Transforms over a continuous time-frequency plane (the scalogram) spanning rhythmic frequencies (0.1 to 100Hz) capture the multiple periodicities implied by beats at different temporal relationships. Gabor wavelets have the property of preserving the phase of the frequency components of the analyzed signal. The use of phase information provides a new approach to the analysis of rhythm. Measures of phase congruence over a range of frequencies are shown to be useful to highlight transient rhythms and temporal accents. The performance of the wavelet transform is demonstrated on an example of generated rhythms.