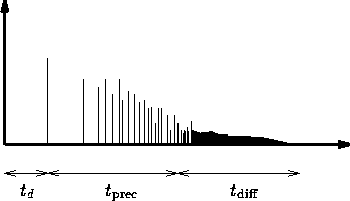
Figure 19: Réponse impulsionnelle type d'une salle
Historiquement, la première application des guides d'onde concernait les tables de reverbérations numériques. L'idée générale consiste à réaliser un dispositif numérique qui reproduit artificiellement une sorte d'effet de salle. D'un point de vue pragmatique, il convient d'examiner la réponse impulsionelle provenant de l'effet de salle (typiquement la réponse mesurée en un point à un coup de feu tiré dans une salle). On distingue traditionnelement 3 zones (fig. 19), à savoir le son direct, les premières réflexions, et finalement la réverbération tardive, appelée également la diffusion.

Figure 19: Réponse impulsionnelle type d'une salle
La première idée ingénieuse qui vient à l'esprit pour réaliser un dispositif dont la réponse impulsionnelle se comporte de la même façon qu'une réponse impulsionnelle provenant de l'effet de salle, consiste à mettre en parallèle plusieurs filtres en peignes utilisant des retards qui sont à peu près premiers entre eux, comme indiqué sur la figure 20.
On constate que chaque filtre en peigne génère une impulsion tous les
p échantillons. En conséquence, si chaque cellule génère un train
d'impulsions dont les périodes sont premières entre elles, le signal
de sortie n'est plus périodique. La réponse impulsionnelle d'un tel
système est donc constitué dans un premier temps d'une série d'échos
distincts successifs. Après un certain temps, la densité des échos est
telle qu'il ne reste plus qu'un signal diffus: la réverbération
tardive. Au bout du compte, la structure temporelle de l'effet de
salle est reproduite. L'analyse fréquentielle d'un tel système est à
rapprocher de l'analyse modale d'un salle parallélépipédique. La
fonction de transfert de chaque cellule vaut
![]() , ce qui fait apparaître p pôles
uniformément répartis sur le cercle de centre 0 et de rayon
, ce qui fait apparaître p pôles
uniformément répartis sur le cercle de centre 0 et de rayon
![]() . Les pôles (i.e. les résonances) ne sont stables que si
g<1. Or l'analyse modale d'une salle
parallépipédique aboutit précisement à 3 séries de modes dont les
fréquences sont proportionelles
. Les pôles (i.e. les résonances) ne sont stables que si
g<1. Or l'analyse modale d'une salle
parallépipédique aboutit précisement à 3 séries de modes dont les
fréquences sont proportionelles ![]() , où l est la
distance qui sépare deux murs qui se font face. En conséquence, le filtre en peigne reproduit la structure
modale d'une paire de murs distants de
, où l est la
distance qui sépare deux murs qui se font face. En conséquence, le filtre en peigne reproduit la structure
modale d'une paire de murs distants de ![]() , où L
représente la distance que parcourt un front d'onde pendant le laps de
temps qui sépare deux échantillons:
, où L
représente la distance que parcourt un front d'onde pendant le laps de
temps qui sépare deux échantillons: ![]() . Les trois
séries de modes sont obtenus en utilisant en parallèle trois filtres
en peigne dont les caractéristiques dépendent de la géométrie de la
salle parallépipédique.
. Les trois
séries de modes sont obtenus en utilisant en parallèle trois filtres
en peigne dont les caractéristiques dépendent de la géométrie de la
salle parallépipédique.
Les inconvéniants de cette méthode sont divers. Tout d'abord cette
méthode colore les signaux (certaines fréquences sont plus amplifiées
que d'autres). Dans certaines applications de sonorisation, il est
préférable de garder un spectre plat, auquel cas l'utilisation de
cellules passe-tout du type de celle proposée figure 21
est préconisée à la place de cellule de filtres en peigne.
Lexicon![]() utilise une méthode denotée filtre passe-tout en gigogne
(nested allpass filters) pour réaliser leurs cellules
réverbératrices. Elle consiste à remplacer dans la figure
21 le coefficient g par un autre filtre
passe-tout...et ainsi de suite. Pour des raisons d'efficacité (et
au détriment de la mémoire utilisée) il est possible d'intervertir le
coefficient g et la ligne à retard
utilise une méthode denotée filtre passe-tout en gigogne
(nested allpass filters) pour réaliser leurs cellules
réverbératrices. Elle consiste à remplacer dans la figure
21 le coefficient g par un autre filtre
passe-tout...et ainsi de suite. Pour des raisons d'efficacité (et
au détriment de la mémoire utilisée) il est possible d'intervertir le
coefficient g et la ligne à retard ![]() (c'est évident parce que
la fonction de transfert est symmétrique en g et en
(c'est évident parce que
la fonction de transfert est symmétrique en g et en ![]() :
:
![]() ).
).
Il existe d'autres inconvéniants beaucoup plus structurels. Tout
d'abord la constante de temps![]() des
cellules passe-tout et en peigne étant de l'ordre de
des
cellules passe-tout et en peigne étant de l'ordre de ![]() , nous sommes ammenés à utiliser la cellule avec des valeurs
de g proche de 1, ce qui nous place en limite de stabilité. Rien ne
nous garantit que les erreurs de calculs ne vont pas faire sortir un
des p pôles à l'extérieur du cercle unité et faire diverger le
système. De plus, la constante de temps est extrèmement sensible aux
variations du paramètre g. Entre une cellule pour laquelle g vaut
0.99 et une autre pour laquelle g vaut 0.999, les constantes de
temps sont dans un rapport 10.
, nous sommes ammenés à utiliser la cellule avec des valeurs
de g proche de 1, ce qui nous place en limite de stabilité. Rien ne
nous garantit que les erreurs de calculs ne vont pas faire sortir un
des p pôles à l'extérieur du cercle unité et faire diverger le
système. De plus, la constante de temps est extrèmement sensible aux
variations du paramètre g. Entre une cellule pour laquelle g vaut
0.99 et une autre pour laquelle g vaut 0.999, les constantes de
temps sont dans un rapport 10.
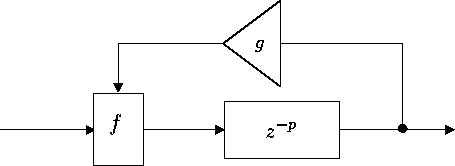
Figure 22: Schéma idéal prenant en compte les erreurs de calculs
D'autre part, toujours à cause des erreurs de calcul, il est possible que la position de repos ne soit pas le seul état stable du système. Les erreurs numériques se traduisent par l'introduction d'une fonction non linéaire dans la boucle idéale (fig. 22). Ce type de schéma (que nous retrouvons dans les modèles physiques d'intruments, voir chapitre 2.4.10) est susceptible d'auto-osciller. Les états stables auto-oscillatants non nuls sont appelés cycles limites et si ce sont des états recherchés dans les modèles physiques d'instruments, ce sont des états à fuire à tout prix dans la synthèse de table de réverbération numérique. Il est parfois possible d'entendre cette auto-oscillation qui refuse de disparaître sur certaines tables de réverbération numérique bon marchée, même en dehors de tout signal d'entrée.
Il est troublant de constater à quel point la structure du modèle de la figure 20 est proche de celle du modèle compact de Karplus-Strong de la figure 10. Il est intéressant, et même utile de voir jusqu'à quel point le rapprochement de ces deux structures peut se faire. Les deux structures sont en fait identiques à un retard près.
Les différences entre les deux modèles interviennent dans l'interprétation que l'on en fait, et dans la manière d'assembler ensemble des cellules. Nous avons vu qu'une cellule représentait une paire de mur. L'interprétation en guide d'onde confirme cette représentation, la longueur du guide d'onde étant l'exact reflet de la distance qui sépare un deux mur. Là où nous nous contentions de sommer la sortie de chacune des cellules, il nous faut à présent, coupler les guides d'onde avec les jonctions adéquates afin de garder une interprétation physiques des signaux qui sont échangés.
L'interprétation physique du système numérique permet de traiter une information énergétique consistante dans le système. Le modèle physique assure que toutes les opérations effectuées dans le système ne rajoutent pas d'énergie et sont au pire dissipatives (par exemple en ce qui concerne les opération arithmétiques en arrondissant en valeur absolue les signaux à la valeure inférieure) ce qui nous assure de ne pas tomber dans des systèmes divergents. De plus il est très facile de rajouter des pertes dans le systèmes (avec un filtre passe-bas par exemple) afin d'éviter de rester coincé dans des états de cycles limites. En outre, les pertes physiques que les signaux acoustiques subissent lors de leur propagation ou de leur réflexion sur les parois s'introduisent très facilement avec les modèle de guides d'onde.
Les guides d'onde facilitent également la construction de réseaux complexes de guides d'onde. Quelque soit l'allure du réseau, le système est garanti de ne pas diverger numériquement.
Il est également possible de rendre dépendant du temps tous les paramètres du réseau (sauf peut-être la structure du réseau) sans risque de divergence ou d'artefact audible. Tout se passe comme si les murs de la salle se déplaçaient en même temps que les signaux sonores se propagaient à l'intérieur de la salle.
Dans le cas d'applications temps-réel (processeurs d'effets sonores par exemple), les modèles de filtres en peignes, filtres passe-tout, et de guides d'onde sont les technologies appropriées et utilisées. Dans le cas de simulations numériques d'effet de salle, les guides d'onde donnent une bonne approximation de la solution par une méthode analogue à la méthode des rayons. Cette méthodologie, quoique rapide et efficace, est évidemment un substitut approximatif par rapport à une simulation totale et complète, par exemple avec un code d'éléments finis, de l'acoustique d'une salle. Elle s'interprète pourtant relativement bien avec une analyse modale de la salle, ou une analyse de l'acoustique en termes de rayons (ray-tracing).