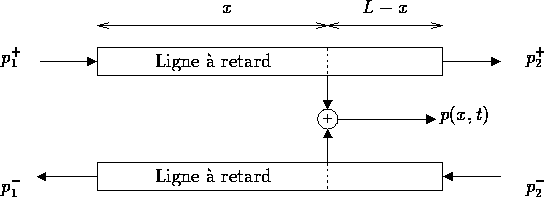
Figure 8: Modèle de guide d'onde sans perte
Contrairement aux modèles précédants où la démarche consistait à approcher au mieux des solutions inaccessibles au calcul algébrique et exactes du système complet, les modèles de guides d'onde discrétisent directement la solution exacte dans le cas de modèles simples. Les modèles plus complexes sont fabriqués par concaténation ou par raffinement successif du modèle de guide d'onde original. On doit la théorie des guides d'onde, appliquée à la synthèse des instruments de musique au professeur J.O. Smith, de Stanford au début des années 1980. Les nouveaux synthétiseurs du commerce dits instruments virtuels (VL1 de Yamaha, Korg Prophecy, Technics WSA1 ...) sont en fait des réalisations industrielles basées sur la théorie des guides d'onde.
Le modèle acoustique le plus simple dont les solutions exactes sont facilement accessibles correspond à la propagation du premier mode transverse d'une onde acoustique dans un tube monodimensionnel (guide d'onde acoustique) sans perte. Le système est régi par l'équation des ondes (19). Dans un tel système, il est toujours possible de décomposer la solution par la superposition d'une onde dite aller et d'une autre onde dite retour. Si les réflexions terminales ne sont pas prises en compte, le système se comporte comme un retard pur pour chacune des ondes aller et retour. Le retard correspond au temps nécessaire à un paquet d'onde pour se propager d'un bout à l'autre du guide d'onde à la célérité c. L'implémentation pratique de ce modèle correspond au schéma de la figure 8. La prise en compte des conditions aux limites correspond à introduire des coefficients des réflexions et de transmittances aux extrémités du guide d'onde. L'implémentation des conditions aux limites se fait conformément à la figure 9 avec le coefficient R de réflexion et T de transmittance. D'un point de vue numérique, quand le retard introduit par le tube est proportionnel à la période d'échantillonage des signaux alors la solution calculée est exactement égale à la discrétisation de la solution originale.

Figure 8: Modèle de guide d'onde sans perte
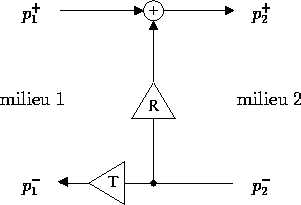
Figure 9: Modèle de conditions aux limites, vues du milieu 2
Physiquement, les coefficients de réflexions sont toujours inférieurs en module à 1. Dans le cas contraire, c'est à dire si l'onde réfléchie est amplifiée à chaque réflexion, cela signifie que les conditions aux limites rajoutent de l'énergie au système au lieu d'en dissiper comme c'est le cas habituellement. Numériquement, cela correspond à utiliser un système qui est susceptible de diverger.
La prise en compte de modèles complets, incluant par exemple des pertes visco-thermiques ou le rayonnement dans l'espace du champs acoustique par le pavillon, n'aboutit pas à une solution analytique explicite. Toutefois l'utilisation de transformées de Fourier et des développement limités permettent d'obtenir des expressions linéaires. Donc au premier ordre, tout s'interprète comme des interconnections de guides d'onde sans pertes, et au second ordre, par des filtres dynamiques, c'est-à-dire par des termes qui dépendent de la fréquence. Or il est connu que la multiplication par un terme dependant de la fréquence dans le domaine spectral (de Fourier) correspond à une convolution dans le domaine temporel, c'est à dire, en terme de traitement de signal à un filtrage.
Les modèles physiques traitées en traitement de signal, sont en fait des modèles qui reproduisent la structure fondamentale du système acoustique en terme de propagation d'ondes, et qui approximent le système physique dans ses détails fréquenciels.
Le modèle de Karplus-Strong est une implémentation particulière
des guides d'ondes sans pertes. Cela correspond à observer l'onde
retour dans un guide d'onde acoustique de longueur ![]() avec comme conditions aux limites une réflexion totale à une
extrémité du guide, et un coefficient de réflexion g à
l'autre extrémité du guide (voir figure 10).
avec comme conditions aux limites une réflexion totale à une
extrémité du guide, et un coefficient de réflexion g à
l'autre extrémité du guide (voir figure 10).
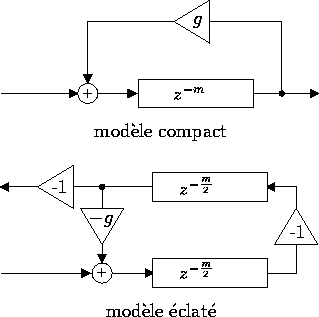
Figure 10: Modèle de Karplus-Strong
Ce modèle fut utilisé à l'origine pour simuler le fonctionnement d'une
corde. En effet, en négligeant la constante de raideur de la corde, en
ne considérant que le mode de transmission transverse des ondes
(c'est-à-dire en négligeant les ondes de pression qui se propagent
longitudinalement dans la corde, ainsi que le couplage des deux modes
qui se propagent sur le plan transverse de la corde), on aboutit au
même système d'équations que celui qui régit la propagation des ondes
acoustiques dans le milieu aérien, à l'exception de la célérité de
l'onde qui dépend à présent de la tension de la
corde. Les conditions aux limites correspondent pour une
extrémité à une réflexion totale c'est à dire à une fixation rigide de
la corde sur le sillet et pour l'autre extrémité ( ![]() ) à
une réflexion presque totale sur le chevalet qui n'est pas
complètement rigide et qui transmet une partie de la vibration à la
table d'harmonie (et réciproquement).
) à
une réflexion presque totale sur le chevalet qui n'est pas
complètement rigide et qui transmet une partie de la vibration à la
table d'harmonie (et réciproquement).
L'utilisation pratique du modèle consiste à initialiser les deux lignes à retard en fonction des conditions initiales de position et de vélocité de la corde. Pour une corde pincée, la position initiale est une position sans vélocité initiale. Cela correspond sur le modèle éclaté à des valeurs initiales dans les deux lignes à retard égales. Dans le modèle compact, cela correspond à une initialisation antisymétrique de la ligne à retard. Pour les cordes frappées, la positions initiale est la position au repos. Donc les valeurs initiales des deux lignes à retard du modèle éclaté sont opposées. Cela correspond à une configuration symétrique pour les valeurs initiales de la ligne à retard du modèle compact.
Dans les deux cas, l'entrée du système reste habituellement à zéro. Cela correspond physiquement à un découplage, artificiel, de la table d'harmonie et du chevalet avec la corde. Physiquement, le couplage entre la corde et le système résonateur est très faible et donc négligeable.
D'un point de vue numérique le système s'interprète comme un filtre
linéaire appelé filtre en peigne dont les propriétés sont bien
connues. La fonction de transfert entrée-sortie du filtre est
![]() .
.
![]()
La réponse impulsionnelle du filtre en peigne est un signal en peigne:
![]() , zéro ailleurs. La réponse en fréquence
présente m pics situés en rapports harmoniques, répartis sur tout le
spectre, qui correspondent à 2m pôles (complexes conjugués) répartis
régulièrement sur le cercle de rayon g. Ce filtre atténue toutes les
fréquences, sauf les fréquences multiples entières de
, zéro ailleurs. La réponse en fréquence
présente m pics situés en rapports harmoniques, répartis sur tout le
spectre, qui correspondent à 2m pôles (complexes conjugués) répartis
régulièrement sur le cercle de rayon g. Ce filtre atténue toutes les
fréquences, sauf les fréquences multiples entières de
![]() (
( ![]() : fréquence d'échantillonage) qui ne sont que
faiblement atténuées.
: fréquence d'échantillonage) qui ne sont que
faiblement atténuées.
Une analyse modale du système physique correspondant aboutit aux mêmes
conclusions. Le système physique dispose d'une infinité de modes, de
fréquences multiples de la fréquence fondamentale ![]() . La
limitation du nombre de mode dans le modèle numérique correspond à
l'hypothèse de limitation de la bande du signal d'entrée: le signal en
entrée est supposé être à bande limitée et donc ne possède pas
d'énergie au-dela de la fréquence de Nyquist (i.e. la demi-fréquence
d'échantillonage), donc les modes supérieurs du système ne sont pas
excités, donc il n'est pas utile de les représenter dans le modèle
numérique.
. La
limitation du nombre de mode dans le modèle numérique correspond à
l'hypothèse de limitation de la bande du signal d'entrée: le signal en
entrée est supposé être à bande limitée et donc ne possède pas
d'énergie au-dela de la fréquence de Nyquist (i.e. la demi-fréquence
d'échantillonage), donc les modes supérieurs du système ne sont pas
excités, donc il n'est pas utile de les représenter dans le modèle
numérique.
Pour comprendre les conséquences de l'initialisation de l'état de
la ligne à retard, il suffit de constater que tout se passe comme si
aux instants ![]() , les valeurs initiales de la ligne
à retard étaient séquentiellement entrées dans le filtre. Donc
l'observation du déplacement du chevalet correspond exactement à
ce que l'on obtiendrait en sortie du filtre s'il était excité,
sur une période de m échantillons par un signal correspondant
au déplacement initial (et à la vélocité initiale) du
système. Cela correspond donc à exciter certains modes du filtre.
, les valeurs initiales de la ligne
à retard étaient séquentiellement entrées dans le filtre. Donc
l'observation du déplacement du chevalet correspond exactement à
ce que l'on obtiendrait en sortie du filtre s'il était excité,
sur une période de m échantillons par un signal correspondant
au déplacement initial (et à la vélocité initiale) du
système. Cela correspond donc à exciter certains modes du filtre.
Dans un premier temps, il faut noter qu'il reste idéaliste que de
supposer que les conditions aux limites n'introduisent pas de pertes
dans le système. En général, les pertes qu'introduisent les conditions
aux limites se manifestent à haute fréquence. En effet, les mesures
expérimentales de coefficients de réflexion (en fait d'impédance
mécanique) sur le rayonnement des instruments à vent ou le mouvement
du chevalet pour les instruments à corde présentent toujours le même
profil passe-bas. Cela conduit à remplacer dans le modèle (voir figure
11) le coefficient g par un filtre passe-bas. Le
système numérique, dissipatif à autre fréquence, le plus simple à
obtenir à partir de ce modèle s'obtient en utilisant le plus simple
des filtres passe-bas: ![]() . On obtient alors le
modèle complet de Karplus-Strong. Ce modèle très simple permet
d'obtenir des synthèses de sons de cordes très convaincant.
. On obtient alors le
modèle complet de Karplus-Strong. Ce modèle très simple permet
d'obtenir des synthèses de sons de cordes très convaincant.
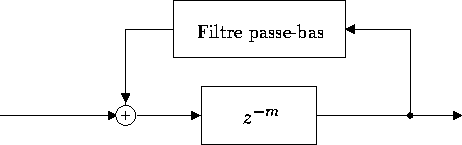
Figure 11: Modèle complet de Karplus-Strong
Il n'est pas toujours possible de pouvoir supposer que les pertes aux
limites se manifestent forcément comme le filtre
![]() . Pour obtenir un système plus proche de la
réalité, il faut faire des mesures acoustiques des coefficients de
réflexion sur un instrument et en déduire le profil du filtre
passe-bas requis.
. Pour obtenir un système plus proche de la
réalité, il faut faire des mesures acoustiques des coefficients de
réflexion sur un instrument et en déduire le profil du filtre
passe-bas requis.
Dans tous les cas, le rajout d'un filtre passe-bas dans la boucle de
rétro-action a pour effet d'atténuer tout à la fois le gain et la
fréquence des résonnances![]() (fig. 12). On constate alors une
certaine inharmonicité dans la répartition des modes de résonnance du
système . Cette inharmonicité correspond
physiquement à l'effet de la réactivité du chevalet (ou du pavillon) à
haute fréquence.
(fig. 12). On constate alors une
certaine inharmonicité dans la répartition des modes de résonnance du
système . Cette inharmonicité correspond
physiquement à l'effet de la réactivité du chevalet (ou du pavillon) à
haute fréquence.
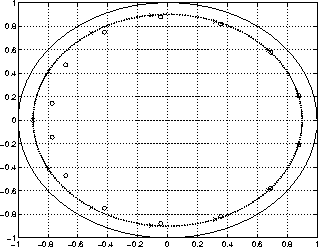
Figure 12: Déplacement des pôles
Il existe en général d'autre sources de pertes, en particulier des
pertes réparties sur toute la géométrie du système oscillant. Par
exemple dans les cordes, les pertes se manifestent également dans le
terme de raideur qui empèche la corde de se plier indéfiniment; dans
les tubes acoustiques, les pertes se manifestent sous formes
viscothermiques, qui traduisent des effets de frottement visqueux et
d'échange thermique important entre les couches du fluide en
oscillation dans le tube et les parois rigides et froides du tube (voir
chapitre 2.4.8). Là
également, les pertes influencent la propagation des ondes
essentiellement à haute fréquence. Il est très couteux en temps de
calcul de tenir compte du caractère réparti des pertes dans un modèle
de guide d'onde, puisque cela revient à répartir m filtres à
l'intérieur de la ligne à retard ![]() . En approximation faibles
pertes, il est toutefois possible de factoriser tous les termes de
perte répartis sur tout le guide d'onde en un seul terme de perte
localisé en bout de guide d'onde. Dans ce cas, cela revient à modifier
le filtre passe-bas évoqué précédemment par un nouveau terme tenant
effectivement compte des pertes réparties.
. En approximation faibles
pertes, il est toutefois possible de factoriser tous les termes de
perte répartis sur tout le guide d'onde en un seul terme de perte
localisé en bout de guide d'onde. Dans ce cas, cela revient à modifier
le filtre passe-bas évoqué précédemment par un nouveau terme tenant
effectivement compte des pertes réparties.
En résumé, le choix habile du filtre passe-bas dans la boucle de rétro-action permet de reconstituer l'effet des pertes dans le guide d'onde et de simuler ainsi l'amortissement plus rapide des partiels de haute fréquence par rapport à ceux de basses fréquence que l'on observe dans la plupart des système acoustique en régime libre.
La seconde limitation du modèle relève de la quantification de la longueur de la ligne à retard. En effet, une fois la fréquence d'échantillonage choisie dont le choix est en général imposé par des critères technologiques (32kHz, 44.1kHz ou 48kHz), la longueur du tubes (ou de la corde) est quantifiée. Par exemple à 32kHz, le pas d'échantillonage spatial pour un tube dans les conditions standarts de pression et de température est de l'ordre du centimètre. C'est l'expression d'une relation d'incertitude . Ce niveau de précision est incompatible avec les exigences des facteurs d'instrument ainsi qu'avec la précision de notre perception auditive. Pour palier cet inconvéniant, il est nécessaire d'implémenter numériquement des dispositifs interpolateurs qui permettent de simuler des retards fractionnaires.
Nous ne rentrerons pas dans les détails d'implémentation des retards
fractionnaires. Dans les grandes lignes, pour un retard réel d, cela
consiste à réaliser un filtre dont la réponse en fréquence est
idéalement ![]() . Parmi toutes les
directions qui s'offrent à nous pour approximer ce filtre, nous n'en
retiendrons que deux: les filtres interpolateurs de Lagrange et les
filtres passes-tout. Comme il est inacceptable pour un modèle physique
que le retard introduise de l'énergie dans le système, le gain en
fréquence du filtre doit constamment être inférieur au gain unitaire.
. Parmi toutes les
directions qui s'offrent à nous pour approximer ce filtre, nous n'en
retiendrons que deux: les filtres interpolateurs de Lagrange et les
filtres passes-tout. Comme il est inacceptable pour un modèle physique
que le retard introduise de l'énergie dans le système, le gain en
fréquence du filtre doit constamment être inférieur au gain unitaire.
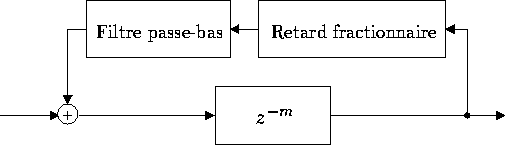
Figure 13: Modèle étendu de Karplus-Strong
Les filtres interpolateurs de Lagrange dérivent des fameux polynômes
interpolateur de Lagrange. Par exemple le filtre passe-bas de
transformée en z ![]() correspond au filtre
interpolateur de Lagrange d'ordre 1 réalisant le retard d'un
demi-échantillon. En effet, ce filtre réalise la demi-somme de deux
échantillons successifs à chaque échantillon, donc on conçoit
facilement que ce filtre réalise l'interpolation linéaire centrée
entre deux échantillons, ce qui correspond à retarder l'ensemble du
signal d'un demi-échantillon. Une interpolation quadratique entre 3
échantillons conduirait à un filtre linéaire d'ordre 2. Les
propriétés de ces filtres sont les suivantes:
correspond au filtre
interpolateur de Lagrange d'ordre 1 réalisant le retard d'un
demi-échantillon. En effet, ce filtre réalise la demi-somme de deux
échantillons successifs à chaque échantillon, donc on conçoit
facilement que ce filtre réalise l'interpolation linéaire centrée
entre deux échantillons, ce qui correspond à retarder l'ensemble du
signal d'un demi-échantillon. Une interpolation quadratique entre 3
échantillons conduirait à un filtre linéaire d'ordre 2. Les
propriétés de ces filtres sont les suivantes:
Les retards fractionnaires passe-tout
découlent de la réflexion suivante: le filtre idéal est
passe-tout, donc il est judicieux d'approximer ce filtre idéal dans
l'espace des filtres passe-tout. De plus, les filtres passe-tout sont
facilement caractérisables puisque leur transformée en z est
toujours de la forme ![]() , où P est un polynôme
d'ordre n. Par exemple pour l'ordre 1, on obtient:
, où P est un polynôme
d'ordre n. Par exemple pour l'ordre 1, on obtient:
![]()
Les propriétés remarquables de ces filtres sont les suivantes:
En résumé, dans le cas où le retard (la longueur du guide d'onde) doit être précis mais invariant temporellement, les filtres passe-tout constituent une solution idéale. Par contre, dans le cas où le retard est assujéti à varier dans le temps, alors les filtres interpolateurs de Lagrange restent un compromis très acceptable. Dans tous les cas, le modèle qui tient compte de toutes les améliorations présentées précédemment est celui présenté en figure 13.
Le problème consiste à trouver une représentation adéquate afin de coupler plusieurs guides d'onde entre eux (voir figure 14). On attend d'une représentation acceptable qu'elle fournisse des principes d'assemblage similaire aux fameuses lois de Kirchoff en électricité.
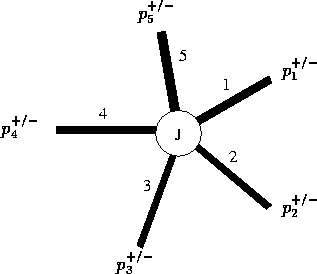
Figure 14: Jonction de n guides d'onde
Nous avons vu au chapitre précédent comment les conditions aux limites
pouvaient s'exprimer en terme de coefficients de réflexions et
coefficients de transmissions (fig. 9). Une telle
analyse peut être menée du point de vue du milieu 2; elle peut être
également menée à partir du milieu 1. Au total, la jonction de deux
guides d'ondes se caractérise par une liste de coefficients de
transmission et de réflexions correspondant aux interfaces entre
chaque milieu (i.e. entre chaque guide d'onde). L'extrapolation du
raisonnement au cas de la jonction de n guides d'onde conduit à une
matrice ![]() dont le terme (i,j) correspond au coefficient
de transmission du milieu i dans le milieu j (et le terme diagonal
(i,i) correspond au coefficient de réflexion du milieu i sur
lui-même). La formulation explicite de la matrice dépend de la nature
des signaux utilisés.
dont le terme (i,j) correspond au coefficient
de transmission du milieu i dans le milieu j (et le terme diagonal
(i,i) correspond au coefficient de réflexion du milieu i sur
lui-même). La formulation explicite de la matrice dépend de la nature
des signaux utilisés.
Les guides d'ondes permettent de représenter tout système physique
dont une des grandeurs physiques est régie par l'équation des
ondes. On a vu que l'élongation longitudinale d'une corde
répondait en première approximation à cette équation. C'est
également le cas des signaux de débit acoustique et de pression
acoustique pour la propagation des ondes acoustiques planes dans un
guide onde acoustique. De façon plus étonnante, le signal de
puissance ![]() satisfait également cette équation.
satisfait également cette équation.
Dans le cas des guides d'ondes acoustiques, les lois qui permettent d'obtenir les équations qui régissent l'interface de n guides d'onde sont celles qui concernent le débit acoustique et la pression acoustique:
Ces équations, dans le cas des jonctions de deux guides d'ondes
conduisent aux expressions suivantes en notant
![]() , coefficient de réflexion
partielle (
, coefficient de réflexion
partielle ( ![]() et
et ![]() correspondent respectivement aux rayons des
tubes 1 et 2):
correspondent respectivement aux rayons des
tubes 1 et 2):
Il est facile, quoique fastidieux, de calculer l'expression de la jonction de n guides d'onde acoustiques. Il apparaît que la jonction est alors caractérisée par n-1 coefficient de réflexion partielle.
Il est important de noter que les lois utilisées (eq. 25) correspondent à des jonctions sans pertes, c'est-à-dire que la jonction est neutre au niveau du bilan énergétique. En conséquence, les algorithmes de jonction ne peuvent pas introduire d'instabilités numériques qui conduisent les calculs à diverger exponentiellement. Il est possible au prix d'un complexité très grandement accrue d'introduire des termes de perte dans les jonctions connectant plus de deux guides d'onde. Par contre, il faut prendre garde de ne pas introduire dans le système des jonctions réactives qui ré-introduisent artificiellement de l'énergie dans le système, et peuvent conduire les algorithmes à exploser numériquement.
Les chapitres précédants ont montré que les guides d'ondes était une alternative efficace pour simuler les systèmes régis par l'équation des ondes. De plus, ce type de synthèse s'insère très facilement dans la théorie du traitement du signal, parque les réseaux linéaires de guides d'ondes peuvent être représentés par des filtres en treillis (fig. 15). Or les filtres en treillis se prètent fort bien à l'analyse auto-régressive avec l'algorithme de Levinson.
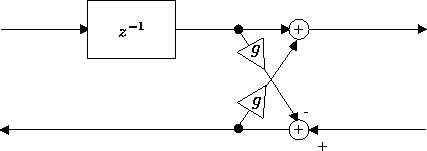
Figure 15: Treilli élémentaire
Structurellement, un treilli élémentaire (figure 15) correspond à un guide d'onde élémentaire, avec une condition aux limites. Le passage du guide d'onde au treilli se fait par une opération simple appelée normalisation. La normalisation dépend de la nature des signaux véhiculés dans le guide d'onde, mais il existe toujours une normalisation qui permet de passer d'un guide d'onde (sans pertes) à un filtre en treillis et réciproquement. Cette correspondance entre les deux modèles à été développée dans les premières études sur le traitement de la parole (1970). Elle permet entre autre d'interpréter le résultat de l'analyse auto-régressive d'un signal de parole comme une modélisation du conduit vocal par un guide d'onde cylindrique de rayon variable.
Nous avons également vu dans le chapitre précédant que
l'introduction de filtres passe-bas permettait de prendre en compte le
caractère résistif de certains éléments acoustiques. Il est
également possible de prendre en compte l'aspect dispersif de la
propagation des ondes dans le guide d'onde en répartissant des
filtres passe-bas dans la propagation du signal, c'est à dire dans
la ligne à retard. Pratiquement les pertes à prendre en comptes
dans un instrument à vent sont les pertes visco-thermiques. Elles
interviennent essentiellement dans des longs tubes![]() du
type tuyau d'orgue. Dans ce type de tubes dit long, il n'est plus
possible de faire une approximation faible pertes (voir chapitre
du
type tuyau d'orgue. Dans ce type de tubes dit long, il n'est plus
possible de faire une approximation faible pertes (voir chapitre
![]() ). L'intensité des pertes viscothermiques est
proportionnelle à
). L'intensité des pertes viscothermiques est
proportionnelle à ![]() , où f est la fréquence. En
conséquence, il faut introduire un filtre numérique dont le gain
s'atténue de 3dB par octave (la moitié du classique 6dB par
octave), ce qui n'est pas standart. Donc pour
introduire les pertes viscothermiques dans les guides d'onde, il faut
répartir des filtres optimisés dans un certaine intervalle de
fréquence, afin que le résultat de la synthèse soit acceptable
dans le même intervalle de fréquence.
, où f est la fréquence. En
conséquence, il faut introduire un filtre numérique dont le gain
s'atténue de 3dB par octave (la moitié du classique 6dB par
octave), ce qui n'est pas standart. Donc pour
introduire les pertes viscothermiques dans les guides d'onde, il faut
répartir des filtres optimisés dans un certaine intervalle de
fréquence, afin que le résultat de la synthèse soit acceptable
dans le même intervalle de fréquence.
Le professeur J.O. Smith a présenté en 1995 (ISMA95) un modèle très convaincant de piano. Chaque corde est représentée par un guide d'onde. En fonction de l'octave, chaque note est simulée par une, deux ou trois cordes couplées, excitées ensemble par la frappe impulsive d'un marteau. L'ensemble des cordes est couplée à la table d'harmonie. La synthèse se réalise en temps-réel sur une station de travail NeXT pilotée par un clavier MIDI.
La modélisation complète d'un instrument de musique doit prendre en compte à la fois le système de propagation de l'onde acoustique, et aussi le phénomène qui est à l'origine de la production du son, c'est-à-dire, soit l'impulsion initiale (corde frappée, corde pincée, membrane frappée), soit le mécanisme auto-oscillant (corde frottée, anche simple, anche double), qui excite l'ensemble du système. Le système complet se décompose dans la grande majorité des cas suivant un ou plusieurs guides d'onde représentant les systèmes propagatifs et résonnants de l'instrument, couplés entre eux et avec un système non lin;eaire régissant les phénomènes transitoires et auto-oscillants. Tous les mécanismes entretenus, tels que le mouvement de la corde frottée par un archet de violon, ou bien le mouvement des cordes vocales, apparaissent alors comme des cycles limites, des attarcteurs étranges de systèmes non lineaires complexes.
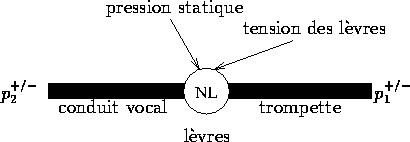
Figure 16: Modèle non linéaire de trompette
L'étude des phénomènes auto-oscillants est loin d'être simple, et les phénomènes sont également loin d'être bien compris. Il est très facile d'obtenir des situations chaotiques, c'est-à-dire dans des situations, en général peu recherchées qui correspondent aux ``canards'' de l'instrumentiste. Le contrôle des paramètres est une tâche ambitieuse et très complexe. La théorie relève plus de l'automatisme (control system) et des mathématiques appliquées que du traitement du signal.
Les modèles d'excitateurs aujourd'hui répertoriés, étudiés et analysés sont aujourd'hui les anches simples, les anches lipales, l'interaction corde-archer, intéraction marteau-membrane ou marteau-corde. Les systèmes d'anche doubles continuent à poser beaucoups de problème de modélisation.
Le système (non-musical) le plus simple qui permet d'engendrer des auto-oscillation est le circuit de Chua (fig. 17 et fig. 18)
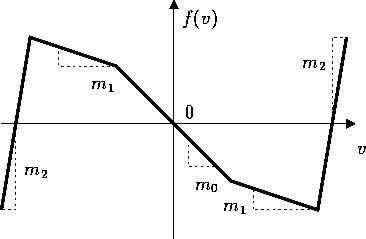
Figure 18: Caractéristique de la diode de Chua