La synthèse par simulation numérique est à l'origine un outil permettant de valider un modèle en comparant son comportement par rapport au comportement naturel du système mécano-acoustique étudié. Dans ce cas, il est plus judicieux de parler de simulations de systèmes physiques plutôt que de synthèses par modèle physique bien que les deux termes soient acceptés. Il est important de noter que la finalité première des simulations n'est pas de réaliser un instrument de musique virtuel, mais uniquement de valider quelques propriétés du modèle. En conséquence les contraintes de réalisation ne sont pas, dans un premier temps, ni des contraintes de contrôle, ni des contraintes de temps réel. Il s'agit d'aboutir à un modèle qui possède le plus de similitudes possibles avec le modèle naturel, afin de pouvoir identifier le modèle à la réalité physique et acoustique du système.
Différents types de conclusions peuvent être tirées des simulations numériques. Elles peuvent par exemple valider un modèle complet et complexe d'un système réel. Le modèle obtenu peut tenter d'expliquer certains comportements inattendus du système physique. Plus important, les simulations permettent de prévoir certains comportements du système réel. La prévision du comportement d'un système est un atout majeur dans les tâches, par exemple, de contrôle des systèmes. Les simulations permettent également de tirer des enseignements sur le soin à apporter à la fabriquation physique du système, tant dans la nature des matériaux à utiliser que dans le soin nécessaire aux opérations d'assemblage. En tout état de cause, il s'agit là d'une démarche très générale, qui tient à la fois du génie scientifique en ce qui concerne l'élaboration du modèle physique, que des sciences de l'ingénieur, en ce qui concerne l'exploitation industrielle du modèle. Ce n'est en aucun une démarche spécifique à l'acoustique, et encore moins à l'acoustique musicale.
En conséquences les techniques utilisées pour la réalisation pratique des simulations sont des techniques très générales, et très largement utilisées, à la fois dans le milieu scientifique et dans le milieu industriel. En général les outils utilisés sont très puissants et précis. En revanche ils sont très coûteux et ne répondent pas exactement aux contraintes citées en début d'exposé. Ils ne tiennent pas non plus compte des quelques degrés de liberté que nous nous accordons en raison des finalités perceptives du signal obtenu. Entre deux méthodes différentes qui génèrent deux signaux différents mais perçus identiquement par notre oreille, il est clair que nous choisirons la méthode la plus simple et la plus rapide. Toutefois, la synthèse par modèle physique complet est souvent un préalable obligatoire avant de pouvoir obtenir un modèle physique efficace, simple et convaincant.
La démarche générale consiste à considérer dans un premier temps le système d'équations différentielles ordinaires (EDO) qui régit le système. La solution algébrique d'un tel système n'est pas en général accessible. Il convient en conséquence de déduire de ce système continu un second système discret dont les solutions sont, à peu de chose près, l'échantillonage (spatial ou temporel) de la solution continue du système original. On dit que l'on propose un schéma de discrétisation pour le système continu.
Il faut bien être conscient, au moment de l'exploitation des simulations, que le schéma de discrétisation n'est qu'un substitut au système original continu; ce n'est pas en toute rigueur l'échantillonage de la solution continue (ou exacte) du système original. Aussi la prudence est-elle de rigueur afin de ne pas confondre les artefacts du schéma de discrétisation (typiquement les phénomènes de dispersion et de stabilité numérique) avec ceux directement liés au modèle physique.
Sans rentrer dans les détails, on peut distinguer deux grandes approches différentes parmis les schémas de discrétisation habituels: les schémas aux différences finies, et les schémas aux éléments finis.
Le schéma aux éléments finis (ou approche variationnelle) consiste à projeter la solution continue de l'EDO sur un ensemble de fonctions de dimension finie (par exemple l'ensemble des fonctions polynômes par morceaux de degré inférieur ou égal à n). Dans ce cas, l'erreur de calcul est évaluée par la norme fonctionnelle de la différence de la solution calculée à la solution exacte (norme au sens fonctionnelle, c'est à dire l'intégrale d'une certaine combinaison linéaire entre la valeur absolue de la fonction et de ses dérivées successives). C'est donc une approximation globale, par opposition au schéma aux différences finies qui constituent une approximation locale.
Le principe des éléments finis s'applique de la façon suivante. Dans
un premier temps, une fonction d'énergie (à valeurs
réelles positives) J est définie sur un espace de
fonction
V de telle
façon que la solution de l'EDO réalise le minimum de J. Ensuite, on
calcule la dérivée de la fonction J. La dérivée de J au
point u, notée 
, est une
application linéaire de V dans 
qui représente la
linéarisation de J au point u. Ce calcul de variation donne son
nom à la méthode dite variationnelle. En réalisant un minimum local,
La solution de l'EDO annulle la dérivée 
. Maintenant on restreint V à un sous-espace vectoriel 
de
dimension finie p (qui dépend par exemple du maillage ou de l'ordre
des polynômes approximants ...). La projection 
de la solution
dans l'espace annulle (dans ) la dérivée de J. Cela
revient à chercher la solution dans qui vérifie
, ce qui aboutit en
général à un système linéaire de p équations à p inconnues.
Considérons l'EDO en v suivante avec des conditions aux limites nulles:
Pour cette EDO, on définit la fonction d'énergie J par l'application suivante:
avec f la forme linéaire et a la forme bilinéaire suivantes:
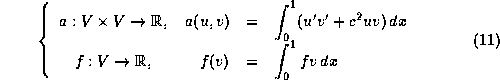
L'application linéaire 
n'est autre que la
linéarisation de J au point u, i.e. la dérivée de J en u. On
vérifie que la solution s de l'EDO originale annule la dérivée,
c'est-à-dire:
Il suffit maintenant de restreindre l'espace V au sous-espace envisagé et de résoudre dans ce sous-espace l'équation (12) qui se ré-écrit matriciellement, une fois qu'une base a été définie:
c'est à dire:
On considère par exemple le maillage régulier de l'intervalle
[0,1] de pas h, et l'ensemble des fonctions polynômiale de
degrée 1 définit par morceaux sur le maillage (c'est-à-dire
affines par morceau). On note ce sous-espace 
. On choisit une
base 
de cet espace (dont on
pourrait facilement obtenir une formulation explicite, voir la figure
5) de façon à avoir:
Il ne reste plus qu'a évaluer A et 
dans ce système de
coordonnées, c'est-à-dire, à calculer 
et 
pour
tous les vecteurs de la base et à résoudre l'équation
(14).
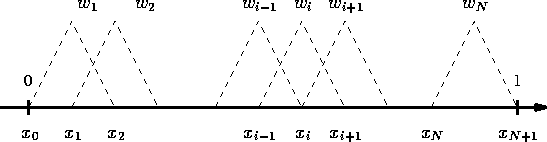
Figure 5: Base de fonctions pour les éléments finis
On suppose par exemple que 
et f sont constant. Dans ce cas
et:
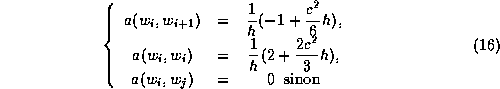
Le schéma aux différences finies consiste à établir un maillage
de l'espace, puis d'évaluer une approximation de la solution sur les
n 
uds du maillage. Il n'est pas nécessaire d'utiliser un maillage
régulier de l'espace, c'est à dire qu'il est tout à fait envisageable
de spécifier en certaines regions intéressantes de l'espace ou du
temps une résolution plus grande (ou le contraire). Une fois le
maillage établi, il est possible de quantifier l'erreur commise
localement sur l'évaluation de la solution en les n uds du
maillage. La méthode repose essentiellement sur des développements de
Taylor, en conséquence, l'erreur est en général majorée par la valeur
absolue d'une dérivée de la solution, donc l'erreur est d'autant plus
petite que la solution est lisse (autrement dit, c'est une
approximation basse fréquence).
Le schéma le plus simple et le plus couramment utilisé reste le schéma
aux différences centrées. Par exemple pour l'EDO de l'équation
(9), sur un maillage régulier de pas h, le schéma
aux différences centrées correspond à substituer v(x) par 
et
v''(x) par 
. Cela correspond à faire des
développements de Taylor à l'ordre 2 et à négliger les termes d'ordre
supérieurs. L'EDO précédante se traduit encore par un système linéaire:
Les modèles des systèmes acoustiques reposent en général sur des
équations différentielles partielles (EDP) incluant des
dérivées spatiales et temporelles. Il est souhaitable d'aboutir à un
schéma numérique dont la solution à un instant donné se calcule en
fonction de la solution aux instants précédants (i.e. un schéma
explicite) par opposition au schéma implicite. Les méthodes numériques
des EDP, pour un schéma explicite donné, imposent des conditions sur
les pas du maillage temporel et spatial
afin que l'erreur de discrétisation ne diverge pas avec le temps. Ce
sont en général des conditions du même type que la relation
d'incertitude d'Heisenberg , qui restreignent le
raffinement simultanné de la résolution du maillage temporel 
et de celui du maillage spatial 
:
L'optimalité, c'est-à-dire, le cas où la dispersion numérique est la
moins sensible, s'obtient en général en maximisant ce rapport
. La dispersion numérique se traduit en
général par un décallage vers le grave des fréquences de résonnances
de la structure simulée par rapport à la structure originale.
Il est également nécessaire d'évaluer la robustesse de l'algorithme vis-à-vis des conditions initiales et des erreurs de calculs. Toutes les variables sont représentées dans les calculateurs soit en virgule fixe soit en virgule flottante. Il découle de cette représentation des erreurs d'arrondi et des erreurs de calculs. Tant que le système n'est pas chaotique (ou du moins tant que le système discrétisé n'est pas chaotique) ces erreurs ne sont pas sensibles. La robustesse des schémas numériques est importante pour pouvoir correctement interpréter les résultats des simulations.
Il est également important de noter qu'il n'existe pas à proprement parler de méthode d'analyse pour de tels modèles physiques, c'est à dire que connaissant la structure du modèle, il est difficile à partir des grandeurs accessibles à la mesure de remonter aux paramètres qui ne sont pas accessibles à la mesure. Autrement dit, il n'est pas possible d'extrapoler systématiquement à partir des observations des paramètres de contrôle qui conduisent à une synthèse aussi proche que voulue de l'original.
Enfin, la structure du modèle discret ne conduit en général à aucune
symmétrie particulièrement remarquable. En conséquence, si la
vectorisation du code est toujours possible (en associant un
processeur de calcul à chaque région de l'espace simulé), la
factorisation du code ainsi que la mise au point d'algorithmes rapides
ne sont pas toujours aisées, et sont même dans la plupart des cas
impossibles. La charge de calcul dépend en principe de la résolution du
maillage spatial, mais comme la résolution du maillage temporel (la
fréquence d'échantillonage) dépend également linéairement de la
résolution du maillage spatial, la charge de calcul requise pour
synthétiser une seconde de son est proportionnelle au carré du nombre
de maille pour les modèles monodimensionnels (cordes, tubes
...). Cela conduit à des modèles numériques assez lents et pas
inutilisables en condition de temps réels.
Prenons par exemple la discrétisation de l'EDP correspondant à l'équation des ondes par un schéma aux différences finies centrées (les conditions initiales sont mises de coté afin de simplifier la présentation):
Le schéma aux différences finies centrées appliqué à cette équation aboutit aux substitutions suivantes (n représente l'index de temps et k représente l'index d'espace):
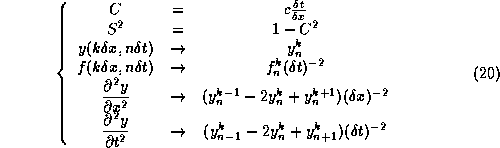
Si on note, 
le vecteur
, alors
l'équation de récurence précédante s'écrit:
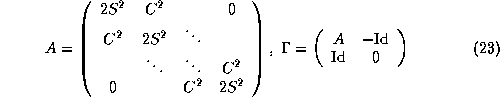
La non-divergence de cette équation de récurence est assurée par
l'inclusion des valeurs propres de la matrice 
à l'intérieur
du cercle unité. La condition 
est suffisante
pour assurer la stabilité numérique du modèle discret.
Comme cité dans un chapitre précédant, les simulations numériques tirent leur source directement de l'étude de la physique du système et proposent des schémas numériques adaptés aux situations.
Prenons par exemple le cas de la simulation de la vibration d'une corde avec terme de raideur. L'EDP qui régit le système est:
Les conditions initiales et les conditions aux limites de cette EDP (qui correspondent à la situation d'une corde encastrée) sont données par:
L'utilisation d'un schéma aux différences finies pour cette
équation conduit à l'équation de récurence suivante, en posant
et 
où N est le
nombre de point du maillage spatial régulier:
L'optimalité vis à vis de la dispertion numérique s'obtient en prenant
. Toutefois la dispersion
numérique liée à ce schéma de discrétisation reste
audible. Il est en fait nécessaire d'utiliser un autre schéma de
discrétisation, dit implicite, beaucoup moins pratique à utiliser afin
que la dispersion numérique ne se manifeste qu'à un niveau inaudible
à nos oreilles.
