Les sons naturels sont en général très fournis en partiels (ou en harmoniques) et il convient de trouver des méthodes pour créer à partir d'un minimum d'oscillateur des sons complexes. La première solution consiste à utiliser une table d'onde constituée d'une période complexe, synthétique ou naturelle et riche en harmoniques. C'est à peu de chose près le principe des échantilloneurs . Les inconvénients liés à cette solution sont multiples: peu ou pas de contrôle du timbre, difficulté de réaliser soi-même des tables d'onde, difficulté de prendre en compte les bruits, impossibilité de synthétiser des signaux non périodiques (percussifs, bruités ou dissonants). Une autre solution consiste à distordre les signaux simples à travers des dispositifs non-linéaires. Une dernière solution consiste à intermoduler le contrôle de période de plusieurs oscillateurs entre-eux. Il s'agit de la modulation de fréquence.
La modulation de fréquence est à l'origine une technique de transmission de signal analogique qui utilise la phase d'une sinusoïde autour d'une fréquence porteuse comme support de l'information. Elle a été introduite en 1936 par E. H. Armstrong .
Au début des années 70, Chowning a le premier tenté d'utiliser et de contrôler ce type de modulation à des fins de synthèses sonores . Il a constaté que si le signal transmis était sinusoïdal, alors les caractéristiques spectrales du signal modulé étaient connues.
À partir des propriétés des fonctions de Bessel de premières
espèces 
, on déduit les propriétés suivantes:
, et disposés symétriquement autour de
la fréquence centrale d'une infinité de partiels situés aux fréquences
. Autrement dit, il se constitue
autour de la fréquence centrale un ensemble de partiels également
espacés, et dont l'espacement vaut la fréquence de la modulante.
. Autrement dit,
l'enveloppe spectrale dépend uniquement de la valeur de l'indice de
modulation.
.
tendent vers 0 quand k tend vers
l'infini. En conséquence, l'energie est concentrée autour de la
fréquence porteuse. En particulier, pour les faibles valeurs de
, seuls les deux premières fonctions, 
et 
, ne sont
pas négligeable (et valent respectivement 1 et 1/2).
Quelques cas particuliers dans la synthèse par modulation de
fréquence appliquée à la musique sont susceptibles de nous
intéresser. Quand la fréquence de modulation est un multiple
simple de la celle de la modulante ( 
), le
signal obtenu est la somme de partiels dont les fréquences sont
toutes multiples d'une fréquence fondamentale. Donc le signal obtenu
est un signal harmonique , dont la fréquence
fondamentale est un sous-multiple de la fréquence de la
modulante .
Dans le cas où la fréquence de la porteuse est exactement le double de celle de la modulante, m = 2 p , alors le signal est harmonique, sa fréquence fondamentale est la fréquence de la modulante, mais toutes les harmoniques paires sont absentes. Il apparaît qu'il s'agit d'une caractéristique commune à tous les sons de clarinettes. En conséquence ce paramétrage constitue un moyen relativement simple pour synthétiser des sons dont la consonnance rappelle celle des sons de clarinettes.
Dans le cas où la fréquence porteuse et la fréquence modulante ne
sont pas dans un rapport simple (par exemple un rapport irrationnel ou
dont le dénominateur est trop grand), le signal obtenu est
inharmonique. Le degré d'inharmonicité se
contrôle en modifiant faiblement le rapport de la porteuse à la
modulante autour d'un rapport simple. La synthèse par modulation de
fréquence apparaît donc comme une méthode très efficace pour générer
et contrôler des sons plus ou moins inharmoniques tels que la plupart
des sons de percussions, de cloches et même dans une certaine mesure
les sons de pianos
.
Rappelons en outre que la synthèse s'effectue dans le domaine numérique. Donc non seulement les partiels de fréquence négative se replient sur la partie positive du spectre , mais les partiels situés au-delà de la fréquence de Nyquist se replient également dans le spectre réel. En raison de cet effet d'aliasing, des partiels harmoniques mal atténués dans la partie haute du spectre sont susceptibles de se replier en partiels inharmoniques avec ceux déjà présents dans le spectre, et contribuer à une distortion désagréable du son.
En résumé, en synthèse par modulation de fréquence:
contrôle l'enveloppe spectrale du
son, c'est-à-dire le timbre,
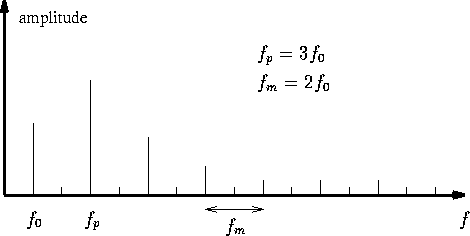
Figure 3: Exemple de spectre issu d'une synthèse par modulation de fréquence
L'inconvénient essentiel de ce type de synthèse, c'est qu'il n'existe pas à nos jours de méthodes d'analyse convaincantes qui permettent d'extraire automatiquement les paramètres de la synthèse, c'est à dire, l'indice de modulation et le rapport de la porteuse à la modulante. En conséquence, la création des sons pour la synthèse FM se fait essentiellement par expérience ou au coup par coup. Par exemple, on sait que la disparition des harmoniques impaires donne un aspect plus ``timbré'' au son.