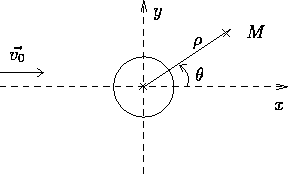
Figure 1: Schéma
On considère un écoulement permanent irrotationnel d'un fluide supposé incompressible autour d'un cylindre de rayon R. Les conditions aux limites à l'infini sont données par la figure 1, c'est-à-dire un champs de vitesse uniforme de direction l'axe des x. La présence du cylindre impose à la vitesse particulaire d'être tangente au cylindre pour tous les points de sa surface.
![]()
![]()
[dsolve].
![]()
[dsolve]:
![]()
[diff]. Considérant que le champs des vitesses doit être
tangent au cylindre pour r=R, déterminer la valeur de B.
les applications numériques et graphiques se font avec
![]() et R=1, en définissant par exemple l'ensemble
et R=1, en définissant par exemple l'ensemble
AN:={v0=10,R=1};
plots[fieldplot]. Pour faire disparaître
le champs de vecteur à l'intérieur du cylindre, on multipliera le
champs de vecteur par
l'expression Heaviside(r^2/R^2-1) qui vaut 0 à l'intérieur du
cylindre et 1 à l'extérieur du cylindre.
On pourra s'aider des instructions suivantes pour le tracé des
isopotentielles de ![]() :
:
> AN := {R=1,v0=10}:
> psi := (r-R^2/r)*sin(theta);
> r_th := solve(psi=cte/5,r);
> r_an1:= subs(AN,r_th[1]): r_an2:= subs(AN,r_th[2]):
> courbe1:={seq([r_an1,theta,theta=0.1..Pi-0.1],cte=0..10)}:cte:='cte':
> courbe2:={seq([r_an2,theta,theta=0.1..Pi-0.1],cte=-10..0)}:cte:='cte':
> plot(courbe1 union courbe2,x=-2..2,y=-2..2,coords=polar);