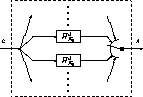
In typical implementations, using LIF in its optimal range (eq. (7)), constrains variations of the delay to remain within a rather restrictive interval. When the delay bypasses these limits, the filter is swapped out for the most appropriate one (fig. 2).
Figure 2: Switch between different filters
As seen in figure 1 our modular structure actually implicitly runs N different filters corresponding to the N first orders. At each time and for any value of the delay, we are free to chose amongst the different filters the most appropriate one without any extra computation. This also means that, for each input sample, we compute the output sample which corresponds to the best approximation of the ideal response. In section 2.7 we have seen that we had the choice between two different filters. From these two filters we use the one which optimizes either the gain or the phase profile according to section 2.6.
Practically speaking, the order of the LIF is dynamically adapted to the most appropriate order whenever the delay bypasses the limits of relation (7) by connecting or disconnecting appropriate modules from the main structure. When the delay is decreasing, two modules are disconnected from the main structure. Inversely, two modules are connected to the main structure when the delay is increasing. The state of these two modules is properly initialized by connecting two supplementary degenerated modules (corresponding to the last loop in the algorithm of table 1) whose function consists in updating the state for the future modules.