


Next: CONCLUSION
Up: DELAY-VARYING IMPLEMENTATION
Previous: LIF Order Adaptation
The previous algorithm cannot limit the order variation
of the LIF without limiting the delay variations. In order to limit
the order variation, we split fractional delay d into a 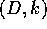 configuration, where d=D+k. This configuration runs a LIF for the
fractional delay D and a classic delay line for the integer
k. Instead of constraining the variation of d, we constrain the
variations of D between a lower and upper limit. Finally we are able
to switch at any time from a
configuration, where d=D+k. This configuration runs a LIF for the
fractional delay D and a classic delay line for the integer
k. Instead of constraining the variation of d, we constrain the
variations of D between a lower and upper limit. Finally we are able
to switch at any time from a 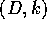 configuration to a
configuration to a 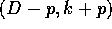 configuration by updating the state of the system in the process
described on figure 3. Since each operation is linear,
the state of the new configuration is actually deduced from the state
of the old configuration through a transition matrix.
configuration by updating the state of the system in the process
described on figure 3. Since each operation is linear,
the state of the new configuration is actually deduced from the state
of the old configuration through a transition matrix.
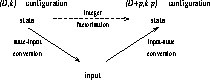
Figure 3: Integer factorisation.
TASSART Stephan
Sat Apr 6 13:58:45 EET DST 1996
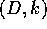 configuration, where d=D+k. This configuration runs a LIF for the
fractional delay D and a classic delay line for the integer
k. Instead of constraining the variation of d, we constrain the
variations of D between a lower and upper limit. Finally we are able
to switch at any time from a
configuration, where d=D+k. This configuration runs a LIF for the
fractional delay D and a classic delay line for the integer
k. Instead of constraining the variation of d, we constrain the
variations of D between a lower and upper limit. Finally we are able
to switch at any time from a 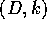 configuration to a
configuration to a 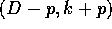 configuration by updating the state of the system in the process
described on figure 3. Since each operation is linear,
the state of the new configuration is actually deduced from the state
of the old configuration through a transition matrix.
configuration by updating the state of the system in the process
described on figure 3. Since each operation is linear,
the state of the new configuration is actually deduced from the state
of the old configuration through a transition matrix.
