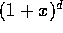 defined over
the
defined over
the 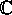 plane minus the real semi-axis
plane minus the real semi-axis 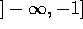 .
Since this function is analytic on its definition domain, it permits a
power series expansion (eq. 4).
.
Since this function is analytic on its definition domain, it permits a
power series expansion (eq. 4).
Now we derive a new recursive expression for LIF by using the power series expansion of the ideal transfer function and by identifying the result to a maximally flat condition LIF.
Let consider function 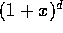 defined over
the
defined over
the 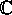 plane minus the real semi-axis
plane minus the real semi-axis 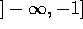 .
Since this function is analytic on its definition domain, it permits a
power series expansion (eq. 4).
.
Since this function is analytic on its definition domain, it permits a
power series expansion (eq. 4).
It is clear that the family of FIR filters, whose transfer function
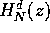 is defined in equation 5, verifies the maximally
flat condition (eq. 3) since they actually are partial
series expansions for
is defined in equation 5, verifies the maximally
flat condition (eq. 3) since they actually are partial
series expansions for 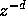 around z=1
(eq. 4). These transfer functions are new expressions
for LIFs.
around z=1
(eq. 4). These transfer functions are new expressions
for LIFs.
This expression may be rewritten recursively (eq. 6). Another nested expression will be useful for the implementation of LIFs (eq. 7).