


Next: Influence of the
Up: LAGRANGE INTERPOLATOR FILTER
Previous: Recursive Expression for
From these expressions, new conclusions about the convergence of LIFs
can be drawn. First of all, from the convergence disk of the power
series expansion, we find that LIFs converge absolutely at low
frequency (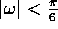 ). Outside of this range,
convergence is not guaranteed. This is not so much a problem since
LIFs are usually only used in their optimal delay range wich is
centered around half the filter order [5]
(eq. 11). Thanks to relation 8, and
because the convergence domain
). Outside of this range,
convergence is not guaranteed. This is not so much a problem since
LIFs are usually only used in their optimal delay range wich is
centered around half the filter order [5]
(eq. 11). Thanks to relation 8, and
because the convergence domain contains the unit circle
(fig. 1), LIFs are guaranteed to converge to the ideal
limit in normal applications (except at the Nyquist frequency).
contains the unit circle
(fig. 1), LIFs are guaranteed to converge to the ideal
limit in normal applications (except at the Nyquist frequency).
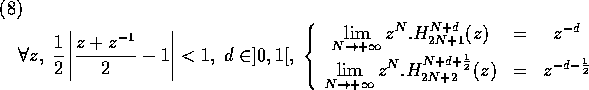
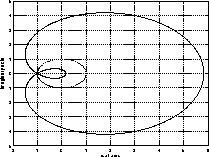
Figure 1: The convergence domain
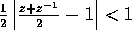 and the unit circle
(dotted line).
and the unit circle
(dotted line).
TASSART Stephan
Sat Apr 6 13:58:45 EET DST 1996
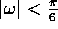 ). Outside of this range,
convergence is not guaranteed. This is not so much a problem since
LIFs are usually only used in their optimal delay range wich is
centered around half the filter order [5]
(eq. 11). Thanks to relation 8, and
because the convergence domain
). Outside of this range,
convergence is not guaranteed. This is not so much a problem since
LIFs are usually only used in their optimal delay range wich is
centered around half the filter order [5]
(eq. 11). Thanks to relation 8, and
because the convergence domain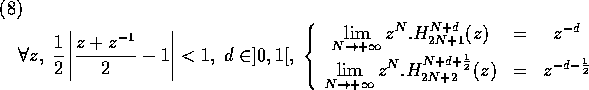

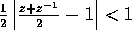 and the unit circle
(dotted line).
and the unit circle
(dotted line).