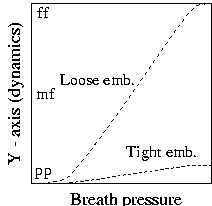
Figure 4: Mapping table for timbral subspace's Y-axis value
In this paper we implement examples of One-to-One and Convergent mapping schemes. In order to develop these mappings, we recorded and analyzed various clarinet performance techniques, including non-standard examples such as overblowing and reed clamping. The couplings are then simulated by processing MIDI data from the controller.
The first example is a simple uncoupled One-to-One mapping, where airflow (breath pressure) data from the WX7 is mapped to overall volume and dynamics, lip pressure is mapped to vibrato, and fingering configuration is mapped to fundamental pitch. 1 In this case we consider the dynamic and volume change to be directly proportional to breath pressure.
With the second example we begin to consider different levels of dependency between parameters in an elementary implementation of Convergent mapping. Thus the input data for the synthesis engine may be dependent on the relationship of two or more gestural parameters. In this example embouchure information acts as a gating threshold for note production, apart from its normal application as a vibrato controller. If the embouchure is not inside a pre-defined range, no note is produced, as is the case with an acoustic instrument.
The third example investigates Convergent mapping further via the relationship between embouchure and breath pressure and their control of note production. Here we implement a "virtual flow" through the reed based on the acoustical behavior explained in section 3 (see Figure 2). (Note that with extremely high breath pressure levels, the loudness will actually decrease, due to the reed blowing closed.) We consider breath pressure data from the WX7 as directly proportional to the pressure inside the mouth, since the reed does not vibrate and the air pressure inside the controller's tube is not influenced by the activation of the keys. This information is sent through two tables, representing curves for loose and tight embouchure values. For all values between these two extremes an intermediate embouchure value is found by interpolation between the tables. For values outside this range, no note is produced. As a result of this coupling, loudness is a function of the "virtual flow." In this example we continue to consider the dynamic interpolation as a direct function of breath pressure.
From the analysis of the recorded clarinet performance technique
examples we noticed that the dynamic interpolation is actually a
function of the breath pressure for a particular
embouchure. This fact leads to our fourth mapping implementation,
where we improve upon example three by taking into account this
interdependency.

Example four (See Figure 4) adds another level of coupling, where variation on the timbral subspace y-axis is controlled by breath pressure, but scaled by the embouchure value. This effect is familiar to wind players when performing a crescendo; one must often progressively loosen the embouchure in order to increase the dynamic. One notices, for example, that for a tight embouchure the actual timbral and loudness variation is very limited. Loosening the embouchure accounts for an increase in both timbral and loudness ranges of our model; the maximum range for the y-axis is reached with a loose embouchure. (This maximum range is equivalent to the difference between pianissimo and fortissimo in our timbral subspace.) It must be noted, however, that although a tight embouchure restricts the timbral and loudness range, it does have advantages. Tightness of the embouchure also controls the timbral quality known to wind players as "focus." Focus appears to be related to the amount of noise component present in the sound; in our model we emulate its effect by varying the amount of noise added to the output.