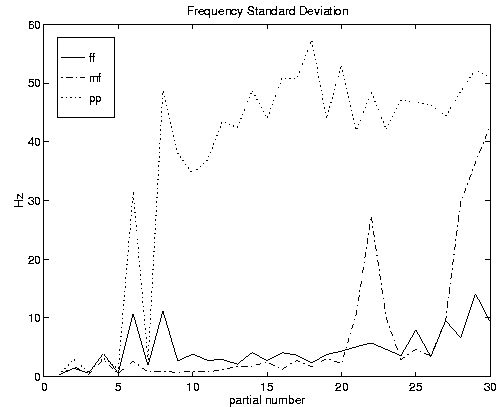
Figure 5: Standard Deviation of the Clarinet's F3 Frequency fluctuations of the first 30 partials in three different dynamics: ff, mf, pp.
In the previous sections we have dealt with various ways to map gestural data in order to improve the espressivity of a controller, applied to a timbral subspace. After analyzing the synthesis results, however, it is evident that problems arise when interpolating between multiple additive models directly derived from sound analysis, such that it is difficult to capture the whole variety of the responsive behaviour of the sound. The purpose of this section is to consider these problems and discuss means to determine the correct synthesis model for interpolation.
Although the additive method allows a variety of transformations, two immediate problems arise in the context of expressivity control:
Let us assume that our system contains only pianissimo (pp) and fortissimo (ff) models. In order to reach an intermediate dynamic model, one morphs between the pp and ff models. In terms of amplitude relations, a close approximation to the mf spectral shape can be achieved by averaging the ff and pp sounds. In terms of the fine temporal behaviour, the situation is different: we observe in the morphed result a strong jitter of the high partials due to the interpolation of the frequency behaviour of the pp partials that are close to the noise floor, thus having a significant frequency jitter, with the originally stable frequency behaviour of the same ff partials. It is important to state that this effect is audibly significant and is heard as some unnatural, distortion-like behaviour of the high frequencies.
Investigating the frequency fluctuations of the three sounds reveals that the standard deviation of the mf sound is not only qualitatively closer to the shape of the ff model, but that the fluctuations in mf are smaller than in the ff sound and they cannot be apporximated by averaging between the pp and ff graphs 2 (see figure 5).

Thus, superimposing wrongly the typical frequency jitter behaviour of the pp with the rather strong interpolated amplitudes creates an undesirable effect which is not present in the original mf sound. Let us now take a closer look at the frequency fluctuations of the partials in the three playing condintions.