On appellera décodeur ambisonics tout décodeur réalisant les points suivants :
) est égale à 1 pour toutes les directions.
Un certain nombre de théorèmes permettent de faciliter le design de décodeurs ambisonics. On trouvera leurs énoncés ainsi que leurs démonstrations dans [Gerzon, 1992]. Nous nous contenterons ici des énoncés.
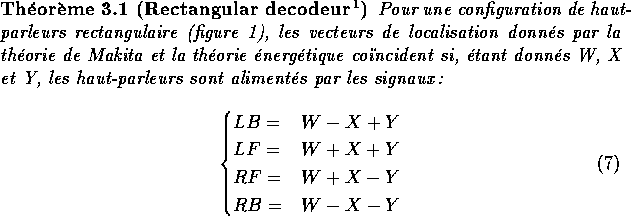
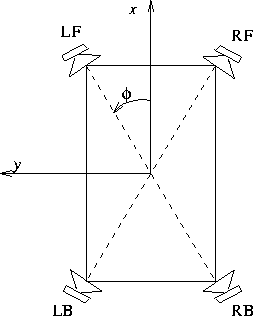
Figure 1: positions et dénominations des haut-parleurs pour les
configurations rectangulaires.
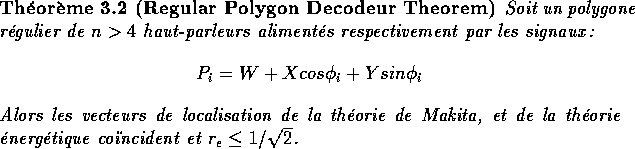
Ces deux théorèmes ont leurs homologues en trois dimensions pour les
configurations de haut-parleurs parallélépipèdiques et polyèdriques (dans
ce dernier cas on a 
).
Ces trois théorèmes sont la base du design des décodeurs ambisonics. La procédure consistant à trouver la formule de décodage en basse fréquence (résolution d'un système linéaire), le théorème approprié assurant alors la validité du résultat pour la théorie énergétique.
Bien que la définition des décodeurs ambisonics soit totalement
indépendante d'un format d'encodage, on associe souvent cette
technique au format B. Ce format est constitué par les quatre signaux
W, X, Y, et Z captés par quatre microphones coïncidants placés
au centre O d'un repère orthogonal 
:
de façon à obtenir (en champs diffus) le même
niveau dans les quatre canaux. Le format B peut être obtenu
également de façon analytique. Pour une onde plane d'amplitude P
provenant de la direction 
(azimut, élévation) les
quatre canaux du format B porterons les signaux :
Pour le format B la résolution du problème en basse fréquence (théorie de Makita) nous donne les deux théorèmes suivants [Gerzon, 1980] :
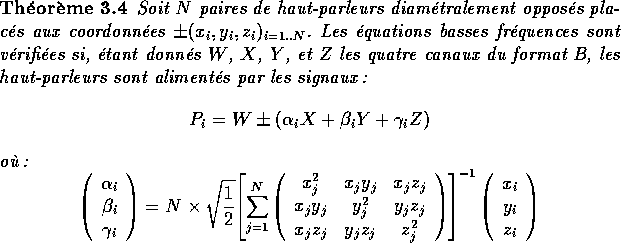
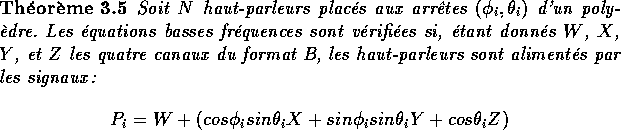
Ces deux théorèmes vérifient les conditions d'égalité des directions
de localisation quelque soit le rapport entre le signal W et les
signaux X, Y, et Z. Il permettent d'obtenir une localisation
parfaite dans les basses fréquences ( 
). Pour optimiser la
valeur de 
on jouera donc sur le rapport entre les 4 canaux
ambisonics en prenant soin de conserver la même énergie totale. Un
décodeur ambisonics construit à l'aide de l'un de ces deux théorèmes
prend donc la forme générique de la figure 2.
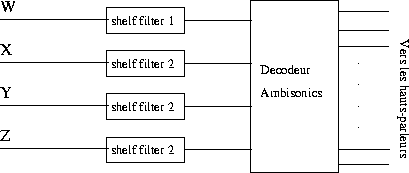
Figure 2: Forme générique d'un décodeur ambisonics pour les
configurations de haut-parleurs opposés par paire ou polyèdrique.
Les shelf filters ont un gain unitaire en dessous de 700 Hz et, au dessus
de cette fréquence, ils augmentent la valeur de W et diminuent
celle des canaux X, Y, et Z de façon à augmenter .
Nous présentons ici les décodeurs que nous avons implémentés dans le Spatialisateur. Tous les décodeurs sont prévus pour recevoir des signaux au format B (équation(8)). Ces signaux étant, soit issus d'une prise de son soundfield, soit calculés à l'aide d'un des codeurs implémentés dans le Spatialisateur : Pan a3 pour les versions horizontales, et Pan a4 pour les versions en trois dimensions. Les décodeurs sont implémentés sous forme de modules Out, l'argument dépendant du décodeur souhaité. Ainsi, le module Out 3a5 décode le format B horizontal (3 canaux) pour une configuration à 5 haut-parleurs (pentagone).
Ce décodeur est adapté pour toutes les configurations de haut-parleurs rectangulaires (cf. figure 1). La formule de décodage en basse fréquence est la suivante :
avec :
Ce décodeur génère les lois de panpot présentées à la figure 3. En remplaçant les valeurs de W, X, et Y dans l'équation (9) on obtient :
ainsi, l'amplitude d'alimentation maximum d'un haut-parleur a lieu
lorsque l'angle de panpot est égal à 
. Pour le cas de
notre figure, le maximum d'amplitude pour le haut-parleur placé à 30
degrés à lieu quand l'angle de panpot est de 60 degrés. On remarque
également sur cette figure la conséquence directe du théorème des
décodeurs pour haut-parleurs opposés par paire ; à savoir que
lorsqu'un haut-parleur est à son maximum d'amplitude , le haut-parleur
opposé est lui à son minimum, donc déphasé de 
.
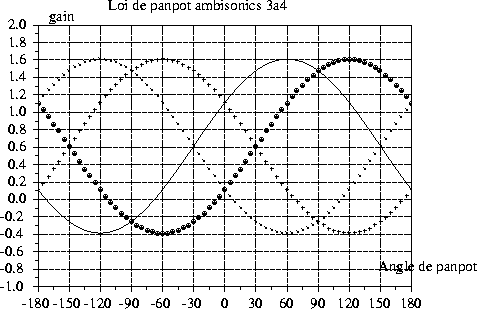
Figure 3: Loi de panpot en basses fréquences pour les quatre
haut-parleurs d'une configuration rectangulaire. L'angle entre les deux
haut-parleurs frontaux étant de 60 degrés ( 
). 
,
, 
, 
.
Nous ne présenterons pas les résultats pour l'angle de localisation
puisque par construction, il correspond à l'angle de panpot en basse
et haute fréquences, ni la norme du vecteur vitesse (velocity
magnitude) puisque qu'elle vaut 1 pour toutes les directions. Pour
maximiser la norme du vecteur d'intensité, il est nécessaire de
modifier les amplitudes respectives des signaux W et X et Y. Les
coefficients d'amplification des shelf filters permettant de maximiser
sont les suivants :
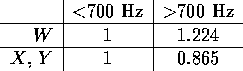
ces coefficients assurent d'autre part de garder un niveau d'énergie constant entre les hautes fréquences et les basses fréquences :
La figure 4 présente la norme du
vecteur d'énergie .
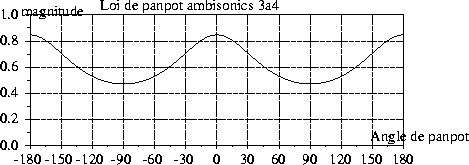
Figure 4: Norme du vecteur d'énergie ( ) pour une configuration
rectangulaire. L'angle entre les deux haut parleurs frontaux étant
de 60 degrés.
Il est intéressant de noter que, alors que pour une configuration
carrée, cette quantité vaut invariablement 
pour tous les
angles de panpot, ici, elle varie dans des proportions non négligeables
donnant lieu à une précision maximale de la localisation à 0 et à 180
degrés.
Ces décodeurs sont adaptés pour les configurations pentagonales, hexagonales, heptagonales, et octogonales. La formule de décodage pour un polygone à N cotés en basse fréquence est la suivante :
avec :
Ce décodeur génère les lois de panpot présentées à la figure 5 (pour un pentagone). En remplaçant les valeurs de W, X, et Y dans l'équation (9) on obtient :
Ici, contrairement aux décodeurs rectangulaires, l'amplitude maximale
d'alimentation d'un haut parleur a lieu lorsque l'angle de panpot est
égal à l'angle du haut-parleur ( 
). Comme pour les
décodeurs rectangulaires, pour les angles de panpot correspondant à une
position de la source opposée par rapport à celle du haut-parleur,
l'alimentation du haut-parleur se fait en opposition de phase.
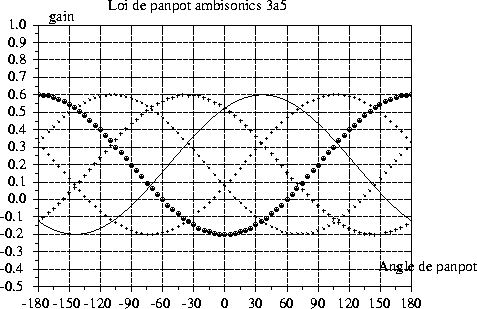
Figure 5: Loi de panpot en basse fréquences pour les cinq
haut-parleurs d'une configuration pentagonale. ,
, , , 
.
Comme pour le décodeur rectangulaire, le principe même de construction
des décodeurs polygonaux nous assure l'égalité de l'angle de panpot et
des angles de localisation pour les théories basse et haute
fréquence, ainsi qu'une localisation parfaite en basse fréquence ( ). Le seul paramètre restant à optimiser est donc la précision de
localisation pour les hautes fréquences ( ). Cette optimisation
s'obtient comme précédemment en amplifiant W au détriment de X et Y.
les coefficients d'amplification des shelf filters sont les mêmes que
pour les décodeurs rectangulaires :
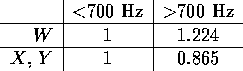
Avec ces coefficients, passe de 0.666 à 0.707. La
figure 6 présente ce résultat pour une configuration
hexagonale. On remarque que comme pour le carré la qualité de
localisation est ici indépendante de l'angle de panpot (re = 1/sqrt2).
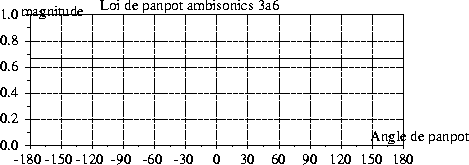
Figure 6: Norme du vecteur d'énergie ( ) pour une configuration
hexagonale.
On obtient donc une qualité de localisation indépendante de l'angle de panpot ce qui aurait tendance à rendre les haut-parleurs moins présents.
