2. Représentation interne des structures musicales
OpenMusic est avant tout un environnement de programmation visuelle, c’est
à dire qu’il permet de résoudre des problèmes, d’effectuer
des calculs, indépendamment de leur domaine d’application en reliant
graphiquement des boites qui représentent soit des données,
soit des fonctions par des lignes qui symbolisent le passage des paramètres.
Cependant, la version de base d’OpenMusic propose une application directe
à la composition musicale en intégrant un formalisme permettant
de représenter des structures temporelles, et plus précisément
des structures musicales de manière symbolique. Cette section décrit
ce formalisme sur lequel vont s’appuyer les opérateurs rythmiques.
2.1 Une organisation hiérarchique
La représentation choisie pour les objets temporels est hiérarchique
: c’est une famille d’objets (au sens de la programmation par objets) qui
permet d’une part de décrire des objets temporels simples, comme
une note, ou un silence et d’autre part des objets de type « contenant
» comme une voix, une polyphonie, un accord, etc. dont la propriété
est de pouvoir contenir soit des objets temporels simples, soit d’autres
contenants.
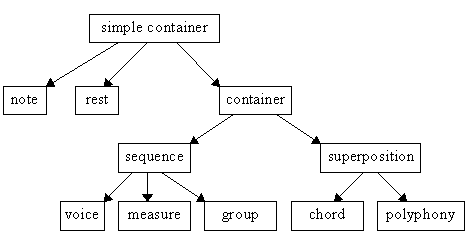Figure 1 : arbre d'héritage des classes
C'est dans la classe simple container que figure la définition
temporelle des objets (donnée dans la section 2.3). Ainsi, toutes
les classes mentionnées dans l'arbre d'héritage, Figure 1,
dérivant de cette classe de base en adoptent les propriétés
temporelles. La classe container, elle, définit la propriété
de ses sous-classes à contenir d'autres objets temporels. La définition
d'une structure musicale s’exprime donc comme un arbre d'imbrications successives
de contenants, les plus globaux en premier, jusqu'aux objets terminaux
de l'arbre qui sont des notes, ou des silences.
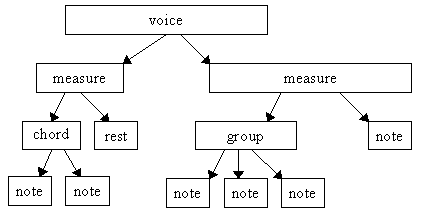Figure 2 : une structure musicale décrite
comme un emboîtement d'objets
A titre d’exemple, la Figure 2 décrit une structure musicale
définie par l’emboîtement d’un ensemble d’objets : à
la base, une voix contient deux mesures. La première est composée
d’un accord de deux notes suivi d’un silence tandis que la seconde est
composée d’un groupe de trois notes suivi d’une quatrième
note. Il n’est, pour l’instant, mentionné aucune description temporelle
dans la définition de cette structure.
2.2 Importance de l'organisation hiérarchique
Un logiciel d’aide à la composition, dont l'utilisation va mener
éventuellement à la réalisation de partitions doit
permettre, dans la mesure du possible, de construire des représentations
satisfaisantes et cohérentes avec la notation musicale. C’est le
cas en particulier lorsque la structure à représenter est
le résultat d’un calcul algorithmique, et dont la représentation
interne ne correspond pas forcement directement à sa représentation
en notation musicale. C’est une des motivations qui incite à choisir
une représentation hiérarchique des structures musicales.
En effet, si l’on souhaite représenter correctement une structure
dans laquelle deux subdivisions irrégulières sont imbriquées,
un triolet dans un quintolet par exemple, il est nécessaire que
la structure soit directement à l'image de cette organisation hiérarchique.
Dans le cas contraire, si le temps était ramené à
une unité unidimensionnelle, il ne serait plus possible de distinguer
les cas où le triolet est emboîté dans le quintolet,
où le quintolet est emboîté dans le triolet, ou encore
où il s'agit d'un quinzolet. De plus, si un quinzolet reste encore
pour certains une subdivision acceptable, que dira-t-on d'un « trentecinqolet
», par exemple, lorsqu'une subdivision par cinq vient s’emboîter
dans une subdivision par sept ? (c.f. Figure 3)
Figure 3 : Deux structures musicalement équivalentes
2.3 Définition temporelle
La définition temporelle des objets tire parti de cette représentation
hiérarchique. Elle utilise un système d’unités locales
à chaque noeud de l'arbre, construit à partir de nombres
entiers qui définissent d'une part une fraction de la noire comme
une unité temporelle, et d'autre part la durée des objets
ainsi que les positions relatives des différents objets contenus,
dans l'unité précédemment établie.
Figure 4 : paramètres temporels d'un objet
de type simple-container
La Figure 4 décrit les paramètres temporels d’un container
simple : le paramètre qvalue représente une fraction de la
noire et définit une unité : si ce paramètre vaut
2, par exemple, l’unité correspondante est la demie noire, c’est
à dire la croche. Le paramètre extent, lui, sert à
exprimer la durée du container, dans l’unité définie
par la qvalue. Si ce paramètre vaut 3, par exemple, avec une qvalue
égale à 2, cela signifie que le container possède
une durée de 3 croches, soit une noire pointée.
Le paramètre offset sert à exprimer la position temporelle
d’un objet : cette valeur ne fait sens que si l’objet est lui même
contenu dans un autre objet de plus haut niveau. La Figure 5 décrit
deux containers eux mêmes contenus dans un container d’ordre supérieur.
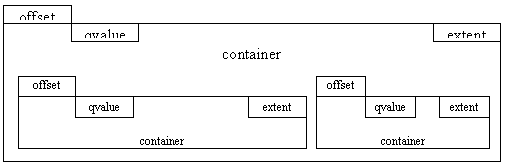Figure 5 : description temporelle dans un emboîtement
Chaque sous container définit donc sa position temporelle dans
le container supérieur par son paramètre offset, s’exprimant
suivant la qvalue du container immédiatement supérieur. Par
exemple, un offset égal à 1 dans une qvalue de 3 définit
une position temporelle correspondant à la deuxième impulsion
d’un triolet de croches.
Cette représentation d’objets temporels possède un certain
nombre de qualités. En particulier, elle permet de définir
de manière exacte toutes les positions . De plus, toute sous-structure
peut être extraite directement en restant toujours cohérante
avec le formalisme et complètement définie au niveau temporel.