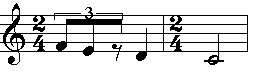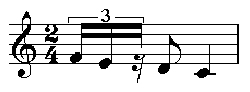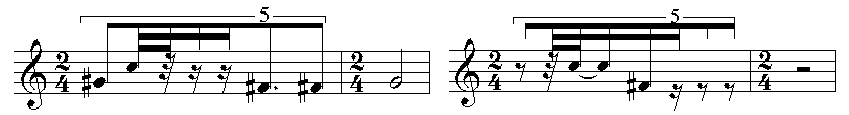index

3. Opérateurs rythmiques

Si le travail sur le domaine des hauteurs a déjà fait l’objet de nombreuses recherches et théories, le domaine du rythme lui est beaucoup moins bien fournit. En particulier, les opérateurs directement appliqués au rythme s’intéressent le plus souvent à un problème précis : la quantification. Cette opération consiste à simplifier un ensemble de données temporelles suivant une unité minimale, créant des distorsions dans les structures musicales mais, en contrepartie, permettant par exemple de les afficher graphiquement ou de corriger les imprécisions temporelles d’un enregistrement Midi [Agon 94], [Assayag 97], [Assayag 94], [Brown 91], [Desain 91], [Vérière 93].

Les opérateurs réalisent des transformations complexes sur les structures musicales sans faire de concessions sur le plan temporel, en mettant à profit l’organisation hiérarchique des structures temporelles intégrée dans OpenMusic.

Nous avons conçu un ensemble d’opérateurs que nous estimons utiles pour les utilisateurs du logiciel. Cette panoplie n’est pas exhaustive, mais elle vise à mettre en évidence un cadre général de travail sur les structures temporelles que l’on pourra éventuellement réutiliser pour la réalisation d’autres opérateurs.

Parmi les opérateurs réalisés, les étirements temporels seront décrits dans la section 3.1 La fusion de structures musicales apparaît en section 3.2. Très proche de cette dernière opération le masquage d’une structure musicale par une autre sera finalement décrite en 3.3.

3.1 Extension / compression temporelle

Les étirements temporels sont un premier type d’opérateurs rythmiques dont la réalisation se prête bien à la définition hiérarchique des objets. Cette opération prend en argument d’une part la structure musicale que l’on souhaite transformer et d’autre part un facteur d’étirement exprimé sous la forme d’un ratio n / p.
Localement, un container muni d’une qvalue q et d’une durée e, étiré d’un ratio n / p a simplement une durée e * n dans une fraction de la noire q * p. Les positions relatives p1,...,pn des éventuels sous containers deviennent alors p1*n,...pn*n dans la nouvelle fraction de la noire q*p

Figure 6 : Description locale de l'algorithme d'étirement temporel

L’algorithme d’extension / compression temporelle parcourt donc récursivement la structure, en profondeur d’abord, en modifiant les champs qvalue et extent des objets, et en mettant éventuellement à jour, pour les containers, les différents offsets de ses sous objets.

3.1.1 Exemple d’étirement temporel

Prenons par exemple, comme structure initiale, la voix décrite Figure 7

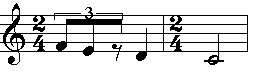Figure 7 : Structure initiale pour l'étirement temporel

Le résultat de la compression temporelle de cette structure initiale par un facteur 1/2 est donné sur la Figure 8 : simplement, les croches de triolet deviennent des double croches de triolet, le demi soupir de triolet devient un quart de soupir de triolet, la noire devient une croche et la blanche devient une noire

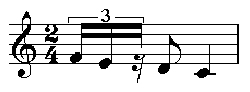Figure 8 : Compression d'un facteur 1/2

Si nous effectuons maintenant un étirement de facteur 3/2 (c’est à dire une extension), la croche de triolet devient une croche et la structure ternaire disparaît.

Figure 9 : Extension d'un facteur 3/2 On remarquera que le résultat obtenu et présenté Figure 9 contient des mesures augmentées. Dans ce cas précis, une simplification était envisageable, en étirant le chiffrage d’un même ratio, c’est à dire en écrivant deux mesures à 3 / 4. Dans des cas plus complexes, le résultat de l’étirement n’est pas toujours facile à représenter en notation musicale.

3.2 fusion de structures musicales :

L’opérateur de fusion prend en argument deux structures musicales et rend comme résultat une structure dans laquelle seront regroupés l’ensemble des éléments terminaux des structures initiales. Lorsque plusieurs notes interviennent simultanément, elles sont regroupées à l’intérieur d’un accord.

Une manière de raisonner pour réaliser cet opérateur consiste à considérer une structure musicale comme étant composée d’une part d’une ossature, c’est à dire la structure initiale privée de ses éléments terminaux, et d’autre part d’une frange, constituée de la liste de ses éléments terminaux.

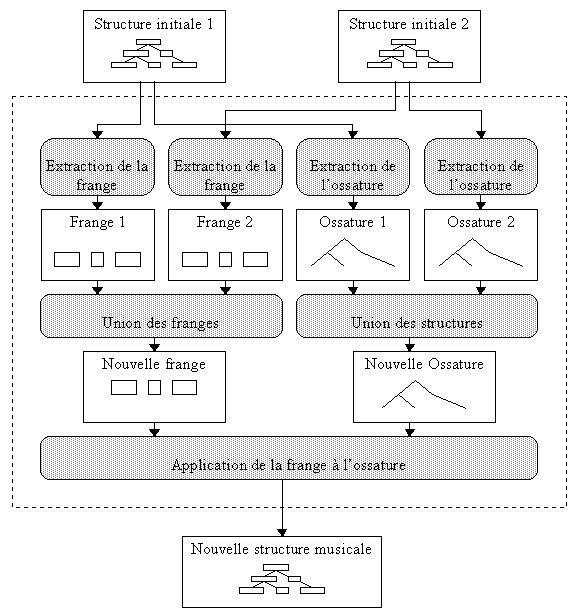Figure 10 : Schéma général de l'opération de fusion A partir de ce point de vue, l’opération de fusion consiste à calculer une nouvelle frange, une nouvelle ossature, et enfin à appliquer cette frange à l’ossature. Le schéma général de cette opération est décrit Figure 10 : les sections suivantes en détaillent les divers composants.

3.2.1 Extraction de l’ossature

L’extraction de l’ossature est une opération simple consistant à parcourir récursivement la structure initiale en supprimant les éléments terminaux. Cependant, l’étape de calcul d’une ossature commune (décrite en 3.2.4) nécessite de détecter les éventuelles subdivisions irrégulières (triolets, quintolets, septolets,...) qui appartiennent à la structure. Or, cette opération n’est possible qu’en examinant chaque container et particulièrement la manière dont son contenu est réparti. Pour que cette opération soit toujours possible à partir des ossatures, les éléments terminaux de la structure initiale sont remplacés par des containers vides (reprenant leurs propriétés temporelles) dans l’ossature extraite.

3.2.2 Extraction de la frange

Au contraire, l’extraction de la frange consiste à construire une liste des éléments terminaux qui se trouvent dans la structure. Pour que l’information soit conservée intégralement, il faut que les offsets des éléments terminaux récoltés soient exprimés de manière globale, et non plus relativement au container d’ordre supérieur qui les contient. De manière récursive, le calcul d’un offset absolu se fait localement par la somme de l’offset local relatif et de l’offset absolu du niveau immédiatement supérieur. Cette règle est appliquée récursivement jusqu’à la racine de la structure pour laquelle l’offset absolu vaut zéro (le paramètre offset de la racine d’une structure n’a pas d’interprétation possible puisque la racine n’est justement pas contenue dans une structure d’ordre supérieur qui en définirait la qvalue).

3.2.3 Calcul de l’union des franges

L’union des franges consiste à rassembler deux franges (données initialement) en une seule. Cet algorithme requiert un minimum de précautions de manière à éviter les chevauchements. En effet, la frange résultante doit pouvoir être intégrée dans un objet de type sequence, qui interdit tout chevauchement dans son contenu. Pour ce faire, les notes présentant une partie commune avec celles de l’autre frange vont être fragmentées (comme décrit sur la Figure 11) de manière à ce que les parties communes puissent être directement intégrées dans un objet de type chord (accord) et que le résultat ne présente finalement plus de chevauchements.

Figure 11 : exemple d'union de deux franges

Dans l’exemple présenté Figure 11, les deux premières notes de la frange 1 ainsi que la première note de la frange 2 sont fragmentées. Deux accords vont être introduits afin que plus aucune superposition n’apparaisse dans le résultat. De plus, les notes qui sont fragmentées lors de cette opération doivent apparaître de manière liée sur le résultat. Il est donc nécessaire de mettre correctement à jour le champ tie (liaison) des différents fragments, qui prend une des trois valeurs : begin (lorsque la note considérée est la première d’une suite de notes liées), continue (lorsque la note est à l’intérieur d’une suite de notes liées) ou end (lorsque la note est la dernière de la suite).

3.2.4 Calcul d’une ossature commune

Cette opération consiste à construire, à partir des ossatures obtenues précédemment par extraction, une ossature commune capable de recevoir et contenir correctement les éléments terminaux résultant de l’union des franges. Une solution naïve consisterai à ne garder que la plus longue des deux ossatures extraites. Cette solution fonctionne correctement tant que les ossatures initiales ne contiennent pas de subdivisions irrégulières (triolets, quintolets, etc.). Lorsque des subdivisons irrégulières sont présentes, il est nécessaire d’en conserver des traces : en effet, lorsque l’on « plonge » directement un triolet dans un quintolet, par exemple, le résultat obtenu se décrit précisément à l’aide de valeurs exprimées en quinzième de sa durée, sur un seul niveau d’imbrication. Le résultat est alors un quinzolet, ce que nous cherchons précisément à éviter (c.f. section 2.2). La solution retenue consiste donc à propager, pour l’exemple précédent, la subdivision par trois à l’intérieur du quintolet. L’ossature ainsi construite est alors préparée à rendre compte d’une imbrication de subdivisions irrégulières (Figure 12).

Figure 12 : Propagation d'une subdivision par 3 dans une subdivision par 5

Suivant cette méthode, une des deux ossatures initiales va devenir englobante. L’autre, dont on propage les subdivisons irrégulières, est considéré comme englobée. Le choix de l’une ou de l’autre ossature comme englobante n’est pas innocent et s’avère relativement délicat dans certains cas : il amène à des résultats équivalents sur le plan temporel, mais différents au niveau de la notation musicale. Cet aspect est mis en évidence dans l’exemple de fusion de structures musicales donné dans la section 3.2.6.

3.2.5 Application de la nouvelle frange à la nouvelle ossature

Pour finir, cette dernière étape consiste à reporter l’union des franges dans l’ossature commune que l’on vient de construire. Cette opération est décrite localement à un container et s’applique récursivement à toute la structure dérivant de ce container. Elle prend en argument une liste d’objets terminaux à insérer. Si le container possède des sous-structures, il commence par passer cette liste successivement à chacune d’entre elles : la liste intégrale est d’abord passée à la première sous structure, puis la liste rendue est passée à la seconde, et ainsi de suite. Finalement le container examine les éléments restant dans la liste rendue par la dernière sous structure, en conserve les éléments qui lui reviennent (les éléments terminaux qui s’insèrent dans son contenu et ne s’insèrent pas dans le contenu de ses sous-structures) et rend le reste comme résultat (éventuellement au container hiérarchiquement supérieur).
La Figure 13 décrit comment l’algorithme d’application d’une frange à une ossature se déroule dans un exemple précis. Nous partons d’une part d’une frange constituée de deux éléments terminaux A et B (des notes), et d’autre part d’une ossature constituée de quatre containers C1, C2, C3 et C4. C’ est imbriqué dans C3, C2 et C3 sont imbriqués dans C1 (c.f. Figure 13, dans laquelle l’axe horizontal représente la position temporelle). L’opération est réalisée en 5 étapes successives en appliquant à chaque fois l’algorithme local, tel qu’il a été décrit précédemment.
Pour que le résultat obtenu dans l’étape 5 soit tout à fait exact, il faut mentionner le contrôle des liaisons musicales puisque les notes A et B ont été fragmentés, d’une part en A1, A21 et A22, et d’autre part en B1 et B2. Cette gestion se fait comme dans le calcul de l’union des franges, en mettant à jour le champ tie des différents fragments.

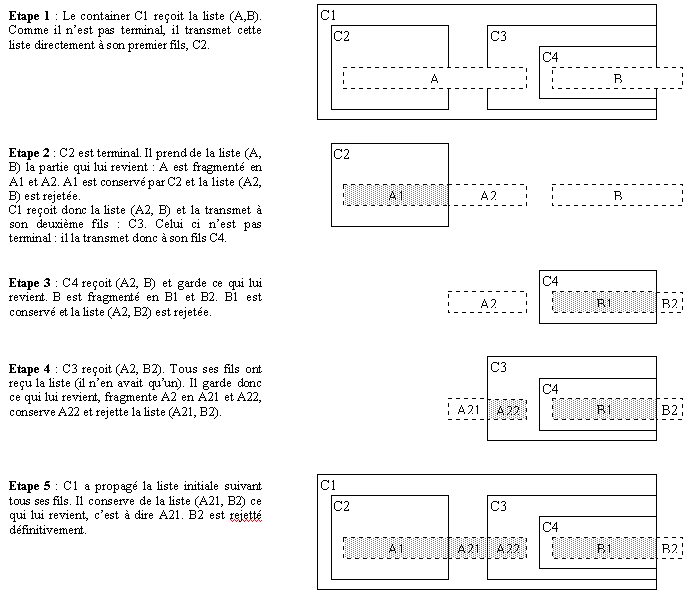Figure 13 : Déroulement de l’algorithme d'application d'une frange à une ossature

3.2.6 Exemple de fusion de structures musicales

Pour terminer nous donnons un exemple de fusion. Les structures initiales sont représentées Figure 14. Cet exemple met en valeur un point important qu’est le choix de la structure englobante et de la structure englobée qui est fait lors du calcul de l’ossature commune (décrit en 3.2.4)

Figure 14 : structures initiales pour l'opération de fusion

La Figure 15 présente le résultat de la fusion des structures initiales de la Figure 14. La mesure de gauche correspond au cas où le triolet est considéré comme englobant, c’est à dire que la subdivision par 5 a été propagée dans la subdivision par trois. La mesure de droite représente le cas contraire, où le quintolet est englobant.

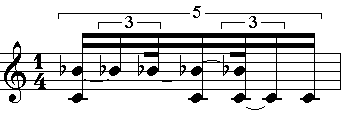Figure 15 : résultat de l'opération de fusion. A gauche, la structure englobante est le triolet. A droite, c'est le quintolet.

Si les deux résultats sont exacts et équivalents du point de vue temporel, celui de droite peut être préférable, car plus simple : dans le résultat de gauche, toutes les impulsions du triolet sont nécessairement subdivisées en 5, tandis que dans le résultat de droite, seuls les deuxième et quatrième impulsions du quintolet sont subdivisées en trois. Dans un cadre général, le choix de l’ossature englobante est une opération délicate à réaliser. En particulier, il peut être nécessaire de la construire à partir de partie de fragments des deux ossatures initiales.

3.3 Masquage de structures musicales.

L’opération de fusion décrite précédemment induit un cadre général de travail pour définir un ensemble d’opérateurs symboliques qui mettent en regard des structures différentes. En particulier, l’opération de masquage d’une structure rythmique par une autre se déduit quasiment directement de l’opération de fusion.

Cette opération consiste à rendre muette une structure musicale lorsqu’une autre est active. Si le résultat correspond à une sous partie de la première structure, celui-ci sera quand même imprégné de l’aspect rythmique de la deuxième. Ainsi, le calcul d’une ossature commune reste nécessaire et est réalisé de la même manière que dans l’opération de fusion. En revanche, le calcul de la nouvelle frange va différer : les deux franges initiales sont extraites comme précédemment, mais l’union des franges est remplacée par le masquage de la première frange par la seconde, illustré Figure 16 par un exemple.

Figure 16 : Masquage d'une frange (donnée) par une autre (masque)

Finalement, comme dans l’opérateur précédent, la structure résultante est calculée comme l’application de la nouvelle frange à la nouvelle ossature.

Figure 17 : Structures initiales pour le masquage. La première sert de donnée et la seconde de masque.

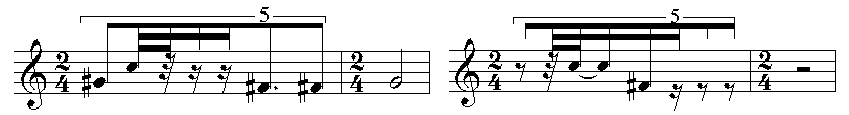Figure 18 : Résultat. La portée de gauche représente l’opération de masquage initiale. Celle de droite correspond au masquage inverse. La fusion des deux résultats permet de retrouver la structure initiale.

Le masquage inverse est réalisé en calculant un masquage des franges avec un opérateur logique différent. C’est un résultat qui peut également s’avérer intéressant : le résultat correspond en fait au masque, dans lequel les hauteurs ont été remplacées par celles de la structure initiale (Figure 18, portée de droite). Il peut être utilisé, par exemple, lorsque l’on souhaite filtrer une trame harmonique à l’aide d’une séquence rythmique.