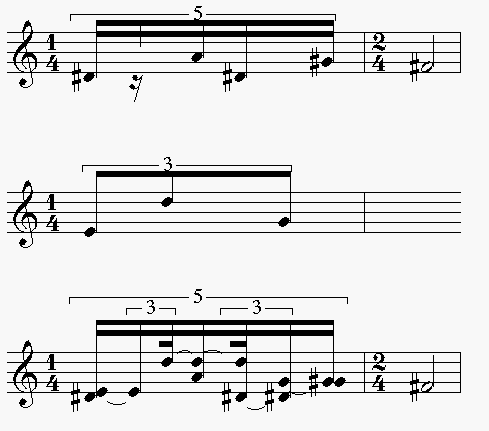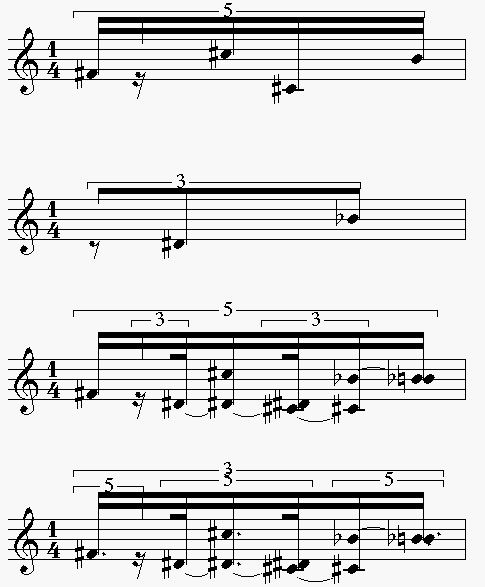Olivier Delerue - Rapport
de Stage de DEA - Etude et réalisation d'opérateurs musicaux
pour un environnement de composition assitée par ordinateur.
III. Développement
Une des grandes faiblesses de PatchWork était son manque de représentations
cohérentes et d'opérations sur le rythme. Une des
raisons de cette insuffisance provient du fait que le travail sur le domaine
du rythme soulève des problème algorithmiques beaucoup plus
importants que pour le domaine des hauteurs. C'est un des points
sur lesquels OpenMusic voudrait innover. Aussi, pour répondre à
une véritable demande des utilisateurs de logiciels d'aide
à la composition, nous avons essayé de définir un
ensemble cohérent d'opérateurs rythmiques qui ont
fortement mis à l'épreuve les structures de données
initialement choisies : à ce sujet, une attention particulière
sera apportée à l'opération de fusion entre
des objets musicaux.
Ainsi, cette section décrit un ensemble de primitives, allant
des fonctions les plus " bas niveau " aux plus évoluées
(accessibles directement à partir de l'interface d'OpenMusic).
Cet ensemble de procédures définit en fait un cadre général
de travail sur les objets musicaux dans lequel d'autres transformations
musicales seront réalisées en n'imposant que des petites
variations au modèle de programmation évoqué.
III.1 Opérations " bas
niveau "
Un ensemble de fonctions bas niveau (c'est à dire complètement
transparentes pour l'utilisateur qui, lui, n'a accès
qu'à des fonctions d'interface haut niveau) est nécessaire
pour pouvoir travailler efficacement sur les structures musicales. En particulier,
le système d'échelles réparties localement
dans la structure et représentées par le paramètre
qvalue de chaque objet peut poser quelques problèmes lorsque l'on
souhaite comparer des structures musicales différentes.
III.1.1 Calcul d'une valeur globale
du paramètre qvalue
La fonction " fraction-minimale " calcule une valeur
de qvalue compatible avec chaque niveau hiérarchique d'une
structure, de manière à proposer une échelle globale
(une fraction de la noire), valable pour l'ensemble de la structure.
Le procédé est simple : il est défini de manière
locale pour un élément de type simple-container, et appliqué
de manière récursive à travers toute la structure.
Si l'objet considéré (de qvalue q) n'est
pas terminal et contient n sous-structures dont des valeurs de qvalue globales
satisfaisantes seraient q1, q2,É,qn,
alors la valeur 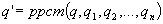 est une fraction de la noire satisfaisante pour pouvoir décrire
pleinement la structure considérée. Si l'objet est
terminal, alors une fraction de la noire satisfaisante est sa propre qvalue.
est une fraction de la noire satisfaisante pour pouvoir décrire
pleinement la structure considérée. Si l'objet est
terminal, alors une fraction de la noire satisfaisante est sa propre qvalue.
Ainsi, la structure est examinée entièrement suivant un
parcours préfixe de l'arbre : à chaque niveau
hiérarchique, ce parcours consiste à consulter les sous structures
dans l'ordre où elles apparaissent (de la gauche vers la
droite sur le schéma).
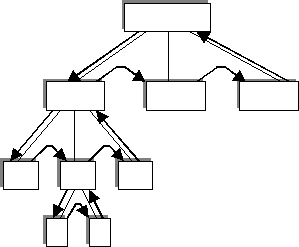
- Parcours préfixe d'une structure
en arbre
Ainsi, la qvalue commune à toute la structure est construite
en remontant des feuilles vers la racine :
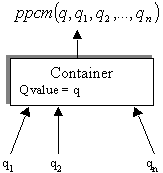
III.1.2 Modification du paramètre
qvalue
La fonction " change-qvalue " se combine généralement
à la précédente : une fois une valeur " qvalue "
globale à toute une structure calculée, on souhaite généralement
réécrire cette structure suivant la nouvelle échelle.
Par le même parcours préfixe de la structure que pour la
fonction précédente, le paramètre qvalue de chaque
élément est remplacé par celui passé en argument
à la fonction. De même, le paramètre extent de l'élément
ainsi que les paramètres offset des objets contenus sont ajustés
par une simple règle de trois.
III.1.3 Réduction du paramètre
qvalue
Cette fonction réalise l'opération inverse aux
transformations précédentes : elle rétablit l'idée
d'une échelle locale en réduisant localement les paramètres
qvalue, extent, et les offset des sous-structures. L'arbre est donc
parcouru en calculant, cette fois ci, des diviseurs communs.
III.2 Vérification d'intégrité
et primitives de formatage pour CMN
Avant d'être confiées à CMN, les structures
musicales sont analysées et ajustées de manière à
correspondre implicitement à leur représentation en notation
musicale. En particulier, les fonctions décrites dans ce paragraphe
réalisent de manière juste certains processus automatiques
de CMN dont le comportement n'est pas satisfaisant dans tous les
cas de figure.
III.2.1 Insertion automatique de silences
Les indications de positions temporelles présentes dans une structure
musicale d'OpenMusic ne sont pas transmises à CMN :
seule une liste de symboles (et de durées) est conservée,
que CMN va représenter graphiquement en les juxtaposant. L'omission
d'un silence dans une structure créerait donc des résultats
catastrophiques lors de sa représentation en notation musicale.
Ainsi, pour qu'une structure musicale soit interprétable
et correctement représentable par CMN, il faut avant tout qu'elle
soit pleine, c'est à dire qu'elle remplisse intégralement
l'espace temporel sur lequel elle est définie.
L'insertion automatique de silences consiste donc à
parcourir intégralement la structure et, à chaque niveau
de profondeur, à insérer des silences là où
l'on trouve des " blancs ". On observe donc,
à partir de chaque élément non terminal de la structure
hiérarchique, comment se réparti son contenu. Lorsque des
" blancs " sont repérés, c'est
à dire que des sous-structures consécutives ne sont pas juxtaposées,
un objet de type " silence " est crée et inséré
en ajustant sa durée de manière à remplir l'espace
vide.
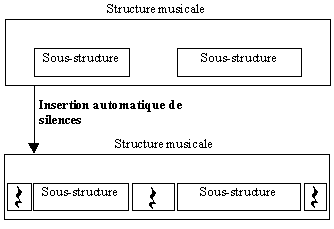
- Effet local de l'insertion automatique
de silences
III.2.2 Insertion automatique d'accords
Cette primitive réalise l'effet dual à la
précédente : des éléments simultanés
dans la structure musicale seront affichés de manière consécutive
(car lus les uns après les autres) par CMN, à moins qu'ils
ne figurent à l'intérieur d'une structure d'accord.
Le même parcours de la structure musicale que dans le cas précédent
est donc effectué, en regroupant les éléments terminaux
simultanés à l'intérieur d'un objet
de type " accord " : on construit alors un niveau hiérarchique
supplémentaire. Bien évidemment, les différents cas
de figure envisageables sont pris en considération : un ensemble
de notes simultanées devient un accord, deux accords simultanés
sont regroupés en un seul accord, un ensemble de notes et un accord
simultanés sont regroupés en un accord également, etc.
III.2.3 Gestion des subdivisions
irrégulières
Comme il était annoncé dans la section concernant
les processus automatiques de CMN, les subdivisions irrégulières
de la noire (triolets, quintolets,...) doivent être spécifiées
explicitement pour être représentées correctement.
Cela signifie qu'il faut être capable, d'une part de
détecter une subdivision irrégulière, et d'autre
part de transmettre des informations aux objets terminaux d'une
structure musicale de manière à ce que leur évaluation
vers CMN produise le chiffrage et les regroupements attendus.
III.2.3.1 Détection d'une
subdivision irrégulière
Le prédicat " tuplet-p " a pour fonction
de déterminer si un objet de type groupe ou mesure est la racine
(au niveau structurel) d'une subdivision irrégulière.
Le résultat de l'appel de ce prédicat est nil (la
valeur " faux " en Lisp) lorsque l'objet n'est
pas la racine d'une subdivision irrégulière, et un
nombre entier dans le cas contraire, correspondant au chiffre qu'il
faut indiquer sur la partition autour de la subdivision irrégulière.
La manière de détecter si un groupe est la racine
d'une subdivision irrégulière est de s'intéresser
à la durée du groupe ainsi qu'à son contenu.
Si l'extent du groupe est une puissance de deux, tous les éléments
contenus se répartissent alors suivant une division " binaire "
du groupe : il n'est donc pas racine d'une subdivision irrégulière.
-
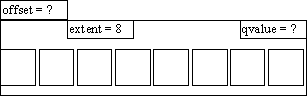
- Dans un groupe dont l'extent vaut 8,
les différents éléments contenus ne peuvent pas s'organiser
suivant
- une division par 3 ou par 5,... Ce n'est
donc pas la racine d'une subdivision irrégulière.
Cependant, ce paramètre extent peut ne pas être exprimé
de manière optimale, éventuellement contraint par le paramètre
qvalue à être un multiple d'un nombre premier : par
exemple si l'extent du groupe vaut 6 et si son contenu est constitué
de deux éléments occupant les positions (offsets) 0 et 3,
la subdivision sous-jacente est directement binaire.
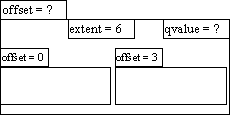
- Un groupe dont l'extent n'est
pas une puissance de deux
- n'est pas forcément la racine
d'une subdivision irrégulière.
Ainsi, de manière générale, repérer
une subdivision irrégulière consiste à détecter
le groupe qui n'est pas une subdivision régulière.
Pratiquement, cela revient à vérifier que le paramètre
extent du groupe considéré, réduit par le pgcd de
l'ensemble constitué de ce même paramètre extent
et des paramètres offset des sous-structures contenues (o1,o2,..ok)
, n'est pas une puissance de deux :
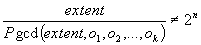
Finalement, l'algorithme se complique légèrement
pour faire face à des cas particuliers. Par exemple, tel qu'il
est décrit, une subdivision irrégulière sera détectée
pour une mesure à 3 / 8, contenant trois croches. Un test supplémentaire
sur le paramètre qvalue est donc réalisé et permet
ainsi d'obtenir les résultats attendus.
III.2.3.2 Propagation à travers la
structure des informations relatives aux subdivisions irrégulières.
Une fois la subdivision irrégulière détectée,
il s'agit de propager, de manière récursive, de la
racine jusqu'aux éléments terminaux, les informations
nécessaires à la mise en forme. Cette opération s'avère
relativement délicate du fait que plusieurs subdivisions irrégulières
peuvent être imbriquées.
On a vu par exemple que pour un triolet, la première note
devra comporter le message (setf
mon-triolet (beat-subdivision- (subdivision 3) ) ), la suivante
: (-beat-subdivision- mon-triolet
) et la dernière : (-beat-subdivision
mon-triolet ) où mon-triolet
est un symbole arbitraire.
Observons le fonctionnement local de cette opération : un
objet groupe reçoit un ensemble de trois listes : début,
continue et fin correspondant aux informations à transmettre aux
objets terminaux qu'il contient, correspondant à d'éventuelles
subdivisions irrégulières dans lesquelles il serait imbriqué.
Si le groupe concerné correspond à la racine d'une
nouvelle subdivision irrégulière, il va à son tour
préparer les informations début, continue et fin qui la concerne.
Puis un appel récursif à cette fonction est réalisé
en propageant les listes début, continue et fin éventuellement
mises à jour avec des informations locales- vers les feuilles de
la structure.
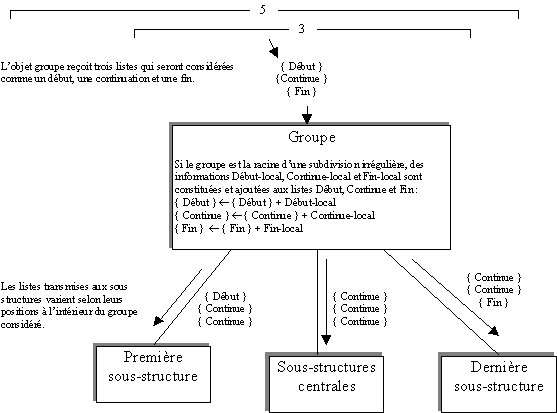
Une précaution reste à prendre cependant, suivant le nombre
d'éléments que contient l'objet considéré :
Si l'objet contient trois sous-structures ou plus, tout se passe
comme indiqué sur le schéma. En revanche si l'objet
ne contient que deux sous-structures, seules les listes correspondant aux
première et dernière sous-structures sont transmises. Pour
finir, si l'objet ne contient qu'une seule sous structure
(ce qui ne devrait pas arriver mais n'est pas gênant
pour autant), les trois listes transmises sont {début} {continue}et
{fin}.
Finalement, les objets terminaux de la structure récoltent les
informations contenues dans les listes et les stockent dans un champs spécial,
rajoutés aux éléments simple-container.
III.2.4 Simplification de structures musicales
Pour finir, une dernière fonction " bas niveau "
est présentée. Celle-ci a pour effet de simplifier les structures
musicales en supprimant des objets de type groupe qui s'avèrent
inutiles : ce sont des groupes ne contenant qu'un seul objet
de taille identique à la leur. Ces objets ne font que compliquer
la structure et leur suppression autorise alors d'autres simplifications.
Par exemple, il peut être intéressant de regrouper deux notes
consécutives et liées en une seule, lorsque leurs durées
sont compatibles (deux croches liées deviennent une noire, une croche
et une noire deviennent une noire pointée,É mais on peut
difficilement regrouper une noire avec une croche de triolet). C'est
donc ce que réalisent respectivement les fonctions " delete-useless-containers "
et " do-grouping "
III.3 Compressions et Etirements
symboliques
L'organisation des objets musicaux en imbrications successives
de contenants et contenus se prête assez bien à ce type de
transformation. Sa définition s'exprime de manière
totalement récursive de la façon suivante : pour étirer
ou compresser dans le domaine temporel une structure d'un rapport
n / p, on ajuste la durée totale de la racine de cette structure
ainsi que les positions relatives des sous-structures contenues et on recommence
cette opération de manière récursive sur les sous-structures,
jusqu'aux éléments terminaux.
Ainsi, pour peu que n et p représentent des nombres entiers,
cette transformation aboutit à une structure déterminée
de façon exacte, sans quantification ni approximation de nombres
réels convertis en entiers.
En effet, si un objet possède une durée d, exprimée
suivant une fraction de la noire (qvalue) q, le résultat de son
étirement devient une durée d * n pour une fraction de la
noire q * p.
III.4 Fusion de structures
musicales
L'opération que l'on souhaite réaliser reçoit
comme données deux structures musicales horizontales (des voix par
exemple) et réalise une nouvelle structure de même nature
reprenant les éléments terminaux (notes, silences) des deux
structures initiales. Cette opération soulève des problèmes
algorithmiques relativement importants.
Le schéma opérationnel de la fusion reste relativement
simple et intuitif : de chacun des deux objets musicaux originaux, on extrait
d'une part une frange, c'est à dire une liste des objets terminaux
de la structure hiérarchique repérés de manière
absolue dans le temps, et d'autre part une structure, c'est à dire
l'objet original privé de ses éléments terminaux.
Deux opérations d'union agissent sur ces paires de franges et
de structures, pour générer, d'une part une nouvelle frange
(constituée donc des éléments terminaux de chacun
des deux objets), et d'autre part une nouvelle structure destinée
à devenir l'ossature du résultat.
Il reste finalement à appliquer cette nouvelle frange à
la nouvelle structure pour obtenir le résultat, fusion des deux
objets initiaux.
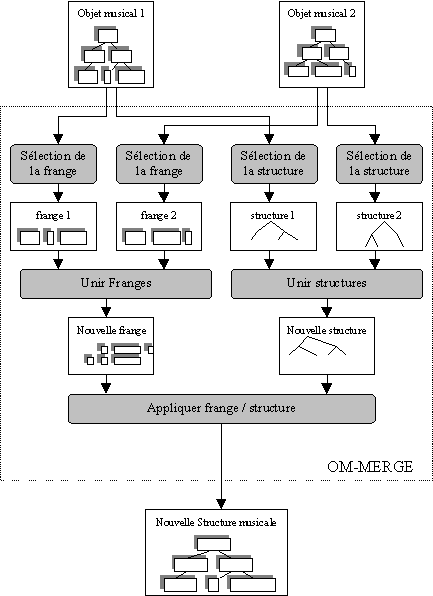
Un premier exemple de fusion mettant en regard un quintolet et un triolet
permet d'avoir une idée sur le type de résultats auxquels
on peut s'attendre. Les deux premières portées sont
les voix originales. La troisième correspond à la fusion
des deux autres :
-
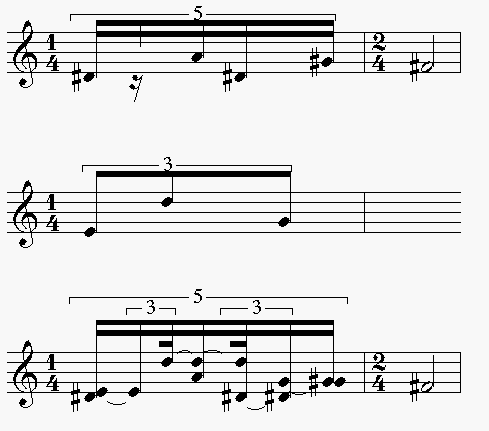
- Exemple de fusion
On remarquera, comme attendu, que des notes apparaissant de manière
simultanée dans les deux voix originales, se traduisent sous forme
d'accords dans le résultat de l'opération.
L'avantage à ce qu'une telle opération
soit réalisée dans le domaine symbolique (c'est à
dire sans passer par une étape de quantification et ramener toutes
les durées à l'échelle de la milliseconde)
est que toutes les données structurelles initiales vont être
conservées dans le résultat.
Observons dans le détail les différents éléments
qui composent cette transformation :
III.4.1 Sélection de la frange
L'opération de sélection de la frange est réalisée
suivant un algorithme classique de l'informatique : c'est
un parcours préfixe de l'arbre, dans lequel on ne garde que
les feuilles. L'opération se concrétise donc par deux
méthodes : l'une s'applique à tous les objets
musicaux (simple-container), l'autre aux objets de type container.
Cette deuxième court-circuite donc la première lorsque elle
peut s'appliquer.
(get-fringe ((self simple-container)) self )
(get-fringe ((self container )) (loop for item in (inside self)
append (get-fringe item)))
Lorsque l'élément de l'arbre considéré
est du type container (une voix, une mesure, un groupe,... ), le résultat
de la fonction est la liste constituée de la concaténation
des résultats de l'application de la fonction get-fringe
à chacun de ses sous-éléments. Lorsque l'élément
n'est pas un container (i.e. une note ou un silence), la fonction
retourne l'élément lui même.
La définition exacte de cette procédure diffère
légèrement de la précédente. En effet, la liste
résultante devra contenir des éléments terminaux dont
le positionnement temporel est exprimé de manière absolue
et non de manière relative à un contenant d'ordre
supérieur. Il est donc nécessaire de dupliquer les éléments
terminaux, en corrigeant sur la copie le champ offset. Pour ce faire il
faut, lors du parcours préfixe, et de manière récursive,
connaître la position absolue du contenant d'ordre supérieur
: current-offset . La position absolue de l'élément
considéré s'en déduit alors facilement par
le calcul (+ current-offset (offset self)). Par ailleurs, il est
impératif que les positions des éléments de la frange
soient exprimées dans une unité commune dont la " fraction
minimale " est le meilleur candidat.
III.4.2 Sélection de la structure
La sélection de la structure est une opération très
similaire à la précédente : on effectue le même
parcours préfixe dans la structure hiérarchique, en ne conservant
cette fois que les éléments non terminaux. En définitive,
la structure originale est dupliquée, en omettant les éléments
terminaux.
Un écart à cette définition générale
reste cependant nécessaire. En effet, une subdivision irrégulière
représentée par un élément hiérarchique
n'est décelable qu'en présence du contenu de
cet élément et de la manière dont il est réparti.
Or, conserver la trace de ces subdivisions irrégulières s'avère
indispensable pour effectuer l'opération d'union des
structures. Ainsi, dans le cas d'un élément représentant
la racine hiérarchique d'une subdivision irrégulière,
les éléments terminaux qu'il contient éventuellement
sont conservés sous forme de groupes.
III.4.3 Union des franges
Cette opération est plus que l'union des deux listes,
triée suivant l'ordre croissant des positions temporelles.
Les notes figurant dans les deux objets originaux apparaîtront dans
l'objet résultat, soit sous forme de note lorsqu'elles
sont isolées, soit sous forme d'accord lorsqu'elles
apparaissent de manière simultanée avec d'autres notes.
Ainsi il est nécessaire, pour pouvoir constituer des accords, que
les notes simultanées aient la même durée et donc d'effectuer
éventuellement une fragmentation de certaines notes pour les ajuster
à des durées plus courtes. Sans rentrer vraiment dans le
détail de la programmation, le schéma suivant illustre la
tâche de cette opération :
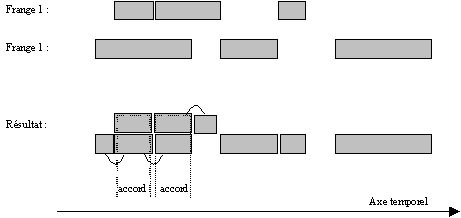
Evidemment, les différents fragments d'une même
note devront être rassemblés par des liaisons musicales.
III.4.4 Union des structures
Le but de cette opération est de proposer, à partir
des structures obtenues par sélection, une nouvelle structure capable
de recevoir et contenir correctement les éléments terminaux
de l'union des deux franges.
Une solution naïve consisterai à ne garder que la plus longue
des deux structures, dans laquelle l'ensemble des éléments
terminaux pourraient s'insérer entièrement. Cette
solution fonctionne en effet relativement correctement lorsque les deux
objets à fusionner ne contiennent pas de subdivisions irrégulières.
Lorsque des subdivisions irrégulières sont présentes,
il est nécessaire d'en conserver les traces. En effet, si
l'on plonge directement les éléments d'un triolet
dans un quintolet, le résultat sera un contenant dont le contenu
se décrit précisément à l'aide de valeurs
exprimées en quinzièmes de sa durée : un " quinzolet ".
En revanche, si l'on propage comme suit la subdivision par trois
à l'intérieur du quintolet, la structure est préparée
pour construire une subdivision ternaire dans une subdivision par 5.
-
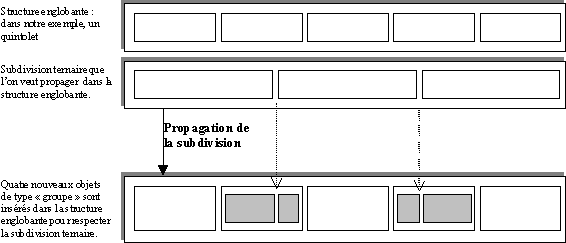
- Exemple de propagation d'une subdivision
par trois dans une subdivision par cinq.
Cependant, choisir de propager les subdivisions irrégulières
de la structure la plus courte dans la structure la plus longue n'est
pas non plus forcément la meilleure solution. En effet, on peut
considérer qu'une des deux structures va devenir englobante
et c'est dans cette structure que seront propagées les subdivisions
irrégulières. Mais le choix de l'une ou l'autre
structure comme englobante amène à deux résultats
différents.
L'exemple suivant illustre ce problème : les deux
premières voix représentent les objets à fusionner,
un quintolet de doubles croches mis en regard avec un triolet de croches.
La troisième portée est la fusion résultante dans
le cas où le quintolet est englobant : la subdivision par trois
est propagée à l'intérieur du quintolet et
le résultat est un quintolet de doubles croches dont les éléments
sont éventuellement divisés en trois. La quatrième
portée représente le cas contraire, le triolet est englobant
et le résultat est un triolet dont chaque élément
est forcément - subdivisé en cinq.
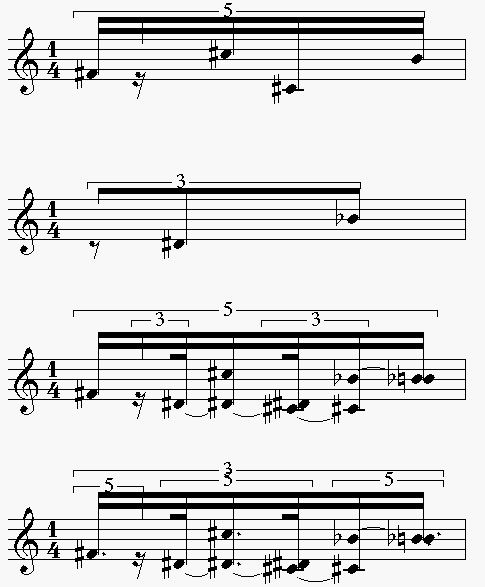
Si du point de vue musical les deux écritures sont exactes,
de manière évidente la première est la plus acceptable
- car la plus simple. L'heuristique sous-jacente veut que l'on
choisisse, lorsque c'est possible, la plus grande des deux subdivisions
comme structure englobante.
Quoi qu'il en soit, la décision de choisir telle
ou telle structure comme englobante (en la prolongeant éventuellement
lorsque la plus courte a été choisie), ou de tenter de construire
une structure plus optimale quand à la simplicité du résultat,
revient à l'utilisateur.
III.4.5 Application d'une frange à
une structure
Cette dernière étape consiste donc à insérer
l'ensemble des éléments que constitue l'union
des franges dans la structure réceptrice. La primitive " applique-liste-structure "
est définie localement et va s'appeler de manière récursive
le long d'un parcours préfixe de la structure finale, en
transportant une liste d'objets terminaux.
Définition locale de la primitive :
Un container reçoit une liste d'objets terminaux a insérer.
S'il possède des sous structures, il va commencer par passer
cette liste à sa première sous-structure (les sous-structures
sont ordonnées suivant leur ordre d'apparition temporel)
: c'est donc un appel à la même primitive, un niveau
hiérarchique plus bas. Le résultat de cet appel contient
tous les éléments que sa première sous structure a
rejetés. Il passe la liste rejetée à sa deuxième
sous structure, puis le rejet de la deuxième à sa troisième,
etc. Lorsque la dernière sous structure a réalisé
son opération, le container récolte dans le rejet ce qui
lui revient (les éléments terminaux qui ne s'insèrent
pas dans ses sous structures mais qui s'insèrent dans son
contenu) et rend le reste des éléments terminaux (au container
hiérarchiquement supérieur qui lui avait confié la
tâche).
Lorsqu'un container récolte les éléments
terminaux qui lui reviennent, plusieurs cas de figure peuvent se présenter
:
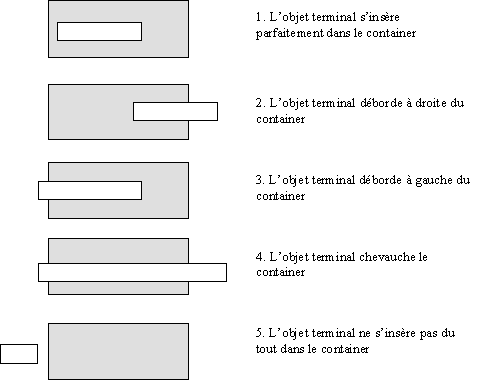
Les cas 1 et 5 sont triviaux : l'objet terminal est soit conservé
(cas 1) soit rejeté (cas 5). Dans les trois autres cas, l'objet
terminal sera fractionné (en deux parties dans les cas 2 et 3, et
en trois parties pour le cas 4) en une partie qui s'insère
dans le container et une (ou deux) parties qui seront rejetées (et
donc retenues par un container d'ordre supérieur ou voisin).
Si l'objet terminal est une note, il faudra alors que ses différentes
fractions apparaissent musicalement liées à l'écran.
Illustrons cet algorithme par un exemple : on suppose que l'on veut
appliquer deux éléments terminaux A et B à une structure
de containers C1, C2, C3 C4 comme suit :
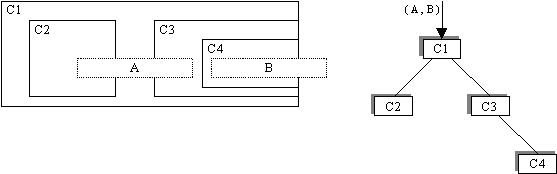
Le container C1 reçoit la liste A, B et, comme il n'est pas terminal,
la transmet directement à son premier fils C2.
C2 est un élément terminal de la structure. Le container
ramasse donc la partie des éléments terminaux qui lui revient
: A est fragmenté en A1 et A2, et B n'est pas touché. C2
garde donc A1 et rejette (A2, B) :
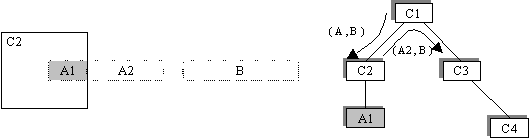
C1 passe ensuite la liste (A2, B) rejetée par C2 à son
deuxième fils C3. Celui-ci n'est pas terminal, donc il fait suivre
la liste à son fils C4.
C4 est terminal, donc ramasse ce qui lui revient. A2 n'est pas touché
et B est fractionné en B1 et B2. Finalement C4 conserve B1 et rejette
(A2, B2) :
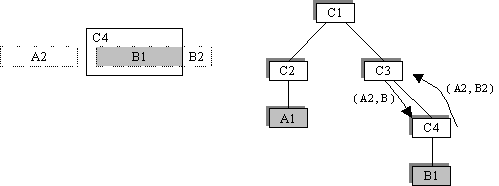
C3 reçoit (A2, B2) de C4 et n'a plus de fils à qui passer
la liste. C3 ramasse donc ce qui lui revient : A2 est segmenté en
A21 et A22. C3 conserve A22 et rejette A21 et B2.
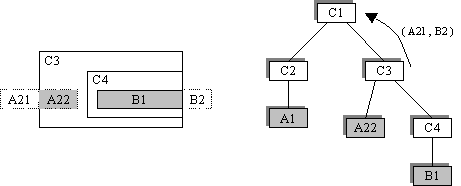
Finalement, le container C1 reçoit la liste (A21, B2) de son
dernier fils. Il conserve donc ce qui lui revient : A21 rentre complètement
et B2 est définitivement rejeté.
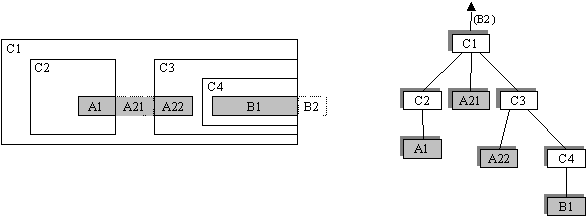
Pour terminer, ce résultat serait exact si A et B étaient
des silences. Dans le cas où A, par exemple, est une note, il faut
lier (au sens musical) ses différentes fractions. Le résultat
est alors :
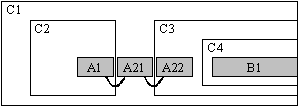
Comment lier les segments de A ? Lorsque A est segmenté
en A1 A2, A n'a encore, a priori, aucune valeur de liaison. A1 reçoit
donc la valeur "début" et A2 la valeur "fin".
Puis, lorsque A2 est segmenté en (A21, A22), A21 reçoit la
valeur "continue" et A22 la valeur "fin".
Le tableau de correspondances suivant permet de déterminer dans
le cas général les valeurs de liaison à assigner au
fragments A1 et A2 en fonction de la valeur précédente assignée
à A :
|
Valeurs de liaison
lors de la fragmentation d'une note
|
|
Ancienne valeur de A
|
Valeur de A1
|
Valeur de A2
|
|
Aucune
|
Début
|
Fin
|
|
Début
|
Début
|
Continue
|
|
Fin
|
Continue
|
Fin
|
|
Continue
|
Continue
|
Continue
|
En conclusion, on comprend aisément que de telles opérations,
respectant la structure rythmique au niveau symbolique, n'aient
pas fait l'objet d'un grand nombre de réalisations
informatiques : l'algorithme sous-jacent à des transformations
qui, du point de vue musical, semblent très simples, est parfois
relativement complexe à mettre en Ïuvre.
III.5 Variantes
Non seulement cette opération de fusion constitue en elle même
un premier type de résultat, mais elle définit également
un modèle de programmation général pour un ensemble
de transformations sur les structures musicales. Ainsi, bien que cela n'ait
pas été prévu initialement, cette primitive s'étend
et s'adapte par de petites modifications dans son schéma
général à toute une classe d'opérations
non dénuées d'intérêt pour le travail
du compositeur.
Entre autres, l'idée de transformation binaire sur des
structures de même nature peut nous suggérer la notion de
masquage, monnaie courante aujourd'hui dans le travail de certains
compositeurs. L'intérêt reste le même que pour
la fusion : le masquage est réalisé de manière symbolique,
ce qui permet de conserver la structure initiale dans le résultat.
Ce que l'on se propose de réaliser est donc une fonction
qui reçoit en arguments deux objets musicaux, de type " voice "
par exemple, et dont le résultat est la première voix masquée
par la deuxième, c'est à dire le contenu de la première
voix aux instants où la deuxième est muette. De la même
manière, on peut envisager l'opération inverse qui
consiste à récolter de la première voix les éléments
apparaissant aux instants où la deuxième est active.
Cette transformation se conçoit très naturellement à
partir de l'opération de fusion : de manière identique
à l'opération de fusion, on commence par extraire
des deux voies originales les franges et les structures. De même,
l'union des structures reste la même. C'est l'opération
sur les franges qui va être légèrement modifiée
: on compare successivement les éléments des deux franges
en supprimant de la première les éléments qui coïncident
avec un élément de la deuxième. Eventuellement, certains
éléments seront fragmentés. Finalement, on applique
la nouvelle frange à l'union des structures.
Le schéma opérationnel du masquage reste donc très
similaire à celui de l'opération de fusion :
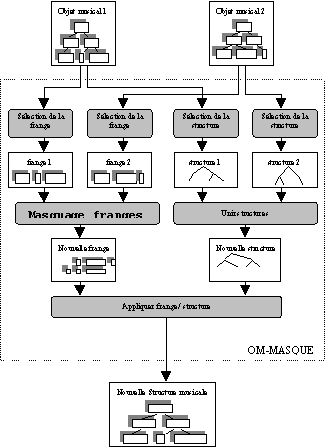
L'exemple suivant illustre cette opération : dans
les deux voix suivantes, la première va servir de donnée
alors que la seconde servira de masque.

Le résultat du masquage de la première voix par
la seconde est le suivant :

Tandis que le masquage inverse, donne ce résultat là
:
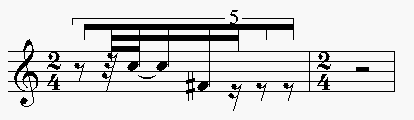
Le détail de cette opération vise à montrer
à quel point l'algorithme de fusion s'adapte facilement
à d'autres transformations : d'autres variantes
suivant le même procédé sont donc envisageables. Pour
le masquage, par exemple, toutes les combinaisons d'opérateurs
logiques amènent à des résultats différents.
De plus, aux contraintes temporelles (rythmiques) du masquage peuvent s'ajouter
des contraintes sur les hauteurs pour produire des opérations encore
plus sélectives. Un certain nombre de ces transformations, ainsi
que des opérations unaires sur des structures musicales (transformations
de type legato, ou, au contraire, repérage d'impulsions)
ont été réalisées mais ne seront pas détaillées.
![]() est une fraction de la noire satisfaisante pour pouvoir décrire
pleinement la structure considérée. Si l'objet est
terminal, alors une fraction de la noire satisfaisante est sa propre qvalue.
est une fraction de la noire satisfaisante pour pouvoir décrire
pleinement la structure considérée. Si l'objet est
terminal, alors une fraction de la noire satisfaisante est sa propre qvalue.