Certains aspects problématiques dans la conception d'un logiciel n'apparaissent parfois pas de manière immédiate. En particulier, la phase d'expérimentation des fonctionnalités décrites dans la section précédente a permis de soulever certaines divergences entre le domaine temporel des objets musicaux et le système de représentation correspondant, la notation musicale.

 Ainsi, à partir d'un exemple précis, cette section soulèvera une problématique complexe à laquelle il faudra forcément mettre un terme. Une méthodologie particulière sera proposée puis, dans le but d'en étendre le domaine d'application, sera envisagée dans un cadre beaucoup plus général. Pour finir, nous évaluerons par une série d'exemples la portée qu'un tel système peut avoir dans un environnement d'aide à la composition.

 IV.1 Problématique

Les manipulations rythmiques définies précédemment permettent de réaliser, par construction ou transformation, des objets musicaux qui, bien qu'étant totalement valides et définis au niveau temporel dans OpenMusic, n'admettent pas de représentation implicite en notation musicale.

Par exemple, que donne l'étirement symbolique d'une mesure simple à quatre temps, composée de quatre noire, par un facteur de 2/3 ? Le tiers d'une noire est une croche de triolet. Les 2/3 d'une noire correspondent donc à une noire de triolet. Ainsi, le résultat de l'opération est une mesure (l'étirement symbolique d'une mesure est une mesure) comportant 4 noires de triolet, ou plus simplement un triolet de noires et une noire de triolet supplémentaire.

Malheureusement, la notation musicale traditionnelle ne fournit pas de moyen pour représenter cette structure : il n'existe pas de signature qui permette d'exprimer quatre noires de triolet dans une mesure.

De manière plus générale, deux grandes catégories de singularités compromettent l'existence d'une représentation symbolique implicite des objets musicaux.

Tout d'abord, si la " qvalue " d'un objet musical, représentant localement la résolution (en terme d'échantillonnage temporel symbolique) nécessaire à sa définition (sa position dans le temps, et la répartition relative éventuelle de son contenu), est illimitée dans la définition interne d'OpenMusic, elle est bornée dans le domaine de la représentation : ainsi, une fraction de la noire trop importante dans une structure musicale amène à une représentation inacceptable car trop complexe, voire impossible.

 L'autre cas, mis en évidence par l'exemple d'étirement symbolique précédent, apparaît lorsque la durée d'une mesure ne s'exprime pas comme un multiple d'une subdivision binaire de la noire. En d'autre termes, cela signifie que la " qvalue " de la mesure vaut 2^p et que son extension est n.

 IV.2 Généralisation

 Que proposer à l'utilisateur qui invoque CMN pour obtenir une représentation musicale de la compression temporelle décrite précédemment ? De manière évidente, il n'existe pas de solution optimale à ce problème. Imaginons cependant cinq transformations, cinq compromis, menant à une structure représentable :

 · Etendre le système de notation musicale : C'est une pratique courante chez certains compositeurs, que l'on retrouve entre autres dans Empreintes de Joshua Fineberg et initiée vraisemblablement par le compositeur Olivier Messiaen. Ainsi, un système de notation autorisant des signatures composées de la forme 2/4 + 1/3 conviendrait parfaitement .

 · Se servir du tempo : La prise en compte du tempo est une méthode qui permet de donner systématiquement une réponse exacte à notre exemple. En effet, un étirement quelconque d'un facteur rationnel de la forme n / p peut toujours s'exprimer de manière exacte en multipliant le tempo par p et en étirant la structure d'un rapport n.

 · Quantifier l'objet musical : Cette opération consiste en fait à forcer la structure musicale à s'écrire suivant, par exemple, une fraction de la noire de la forme 1/2ⁿ. La structure modifiée trouve alors naturellement, dans la notation musicale traditionnelle, une signature correspondante.

 · Etirer ou compresser l'objet musical dans le domaine temporel : De manière relativement similaire à l'opération de quantification, il est possible d'imaginer une manière d'étirer ou comprimer la mesure (dans une limite acceptable) de telle sorte que sa durée symbolique soit compatible avec la notation traditionnelle.

 · Reporter la valeur supplémentaire : Finalement, cette dernière proposition consiste à restructurer l'ensemble de la métrique à partir de la mesure problématique : dans notre exemple, la noire de triolet " en trop " est reportée au début de la mesure suivante. L'opération se répète ainsi jusqu'à la dernière mesure de la voix, éventuellement complétée par des silences.

 Illustrons ce cas de figure en prenant, par exemple, une voix originale constituée comme suit :

 

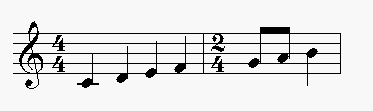
 Compressons la première mesure d'un facteur de 2/3. Le résultat en reportant systématiquement la valeur supplémentaire jusqu'à la fin de la voix est le suivant :

  

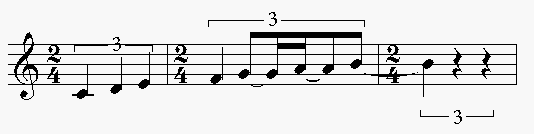
Cependant, une extension du système de notation n'est pas une solution acceptée par tous. La modification du tempo exprimée par un simple changement de tempo dans la partition n'est une solution envisageable qu'à condition que la mesure concernée ne soit pas mise en regard, dans une polyphonie par exemple, avec une autre voix (sauf cas exceptionnel, le tempo est généralement unique à travers les différentes voix d'une polyphonie). De même, la quantification et l'étirement produisent sur la structure une transformation irréversible qui détériore une précision éventuellement nécessaire. Finalement, le report successif de la valeur ajoutée à la mesure suivante déstructure totalement une métrique éventuellement importante car jalonnant l'objet sur des temps forts, par exemple. Ainsi, parmi ces possibilités, aucune n'est utilisable de manière systématique : les facteurs qui interviennent dans le choix de l'une ou l'autre de ces solutions sont principalement les préférences stylistiques de l'utilisateur, et le contexte dans lequel se situe la problématique.

Le problème concernant la " qvalue " est du même ordre : réduire la fraction minimale utilisée à la meilleure valeur acceptable revient à une quantification. Cependant la meilleure valeur acceptable au sens de l'erreur de quantification minimale mène éventuellement à une division binaire d'un objet situé dans un contexte ternaire ou vice versa. De plus, l'ensemble des valeurs acceptables pour la subdivision de la noire n'est a priori pas le même pour l'ensemble des utilisateurs. Les notions de contexte et de préférences d'utilisateurs interviennent donc ici également.

Une expression générale permettant de choisir une de ces solutions semble très complexe sinon impossible à formaliser directement. En effet, dès lors qu'on s'aperçoit que la décision à prendre dépend en partie de l'utilisateur, il n'est plus possible d'envisager une formalisation générale. Il n'est pas non plus raisonnable d'envisager cette formalisation à la place des utilisateurs.

La réponse informatique à ce type de problématique rejoint la notion d'apprentissage. La prise de décision s'effectue alors par la résolution d'une contrainte suivant un système de règles, apprises au " coup par coup ".

 IV.2.1 L'expression de règles de réécriture en Lisp

Une règle de réécriture est une forme du type : A ® B où A est un ensemble conjonctif et / ou disjonctif de prédicats et B un ensemble d'actions à effectuer lorsque A s'évalue à la valeur vrai. Les règles qui nous intéressent ici sont plus précisément de la forme : A(x) ® B(x). C'est à dire que l'on va réaliser l'action B sur l'objet x lorsque la fonction A appliquée à x s'évalue à la valeur vrai.

Le langage lisp est particulièrement bien adapté à la génération automatique de code. Développé à partir de la théorie du lambda calcul, il s'est rapidement imposé dans la réalisation d'applications mettant en ¦uvre des concepts relatifs à l'intelligence artificielle.

 Ainsi, il est relativement aisé d'écrire en Lisp une fonction dont le résultat de l'évaluation est une fonction (ou une méthode). C'est ce que réalise la fonction suivante, dont le résultat de l'évaluation - les méthodes générées - sont des règles de réécriture.

(defun defregle (&key (predicats '(#'(lambda (x) x)) ) 
                          (action #'(lambda (x) x) ) 
                          (type 'simple-container))
    `(defmethod ,(gensym) 
                ((self ,type) &key (mode nil) ) 
                (if (eq mode 'test)
                   ,(append '( and )
                           (loop for pred in predicats 
                                 when (listp pred)
                                 collect (append (list (car pred) 'self ) (cdr pred))
                                 else
                                 collect (list pred 'self))
                           )
                 (if (eq mode 'apply )
                   ,(if (listp action)
                      (append (list (car action) 'self ) (cdr action ) )
                      (list action 'self)
                      ) 
                   (print 'indiquer-mode-fonctionnenement ) 
                  )
                 )
                )
     )

 Cette fonction prend en argument un ensemble de prédicats, un ensemble d'actions ainsi que le type des objets auxquels elle peut s'appliquer. Par exemple, supposons que dans le cas où une mesure a une qvalue de 3 et une extension de 8, il faille la quantifier à la double croche. On écrirait pour définir cette règle :

(defregle :predicats '((qvalue-is 3) 
                       (extent-is 8 )) 
          :action '(quantify 4) 
          :type 'measure )

L'évaluation de cette expression produit la définition suivante :

(DEFMETHOD #:G813 ((SELF MEASURE) &KEY (MODE NIL))
     (IF (EQ MODE 'TEST)
        (AND (QVALUE-IS SELF 3) (EXTENT-IS SELF 8))
        (IF (EQ MODE 'APPLY) 
           (QUANTIFY SELF 4) 
           (PRINT 'INDIQUER-MODE-FONCTIONNENEMENT)
            )
        )
 )

C'est à dire la définition d'une méthode nommée G813 (un nom unique fourni automatiquement par CLOS), qui s'applique à un objet 'self' de type 'measure' et qui nécessite également un mot clef. Lorsque ce mot clef vaut TEST, le résultat de son évaluation est la conjonction des deux tests (QVALUE-IS SELF 3) et (EXTENT-IS SELF 8). Lorsque le mot clef est APPLY, le résultat correspond à l'évaluation de (QUANTIFY SELF 4), c'est à dire à la quantification de notre objet à la double croche.

L'enchaînement des opérations : " si les prédicats sont vrais alors appliquer la règle " s'écrit alors simplement :

(if (apply G813 ma_mesure :mode 'test) 
    (apply G813 ma_mesure :mode 'apply )
    ()
     )  

IV.2.2 Le cas général

L'infrastructure d'un système à base de règles peut sembler démesurée par rapport à l'aspect tellement spécifique du problème à résoudre, bien loin des préoccupations principales d'OpenMusic.

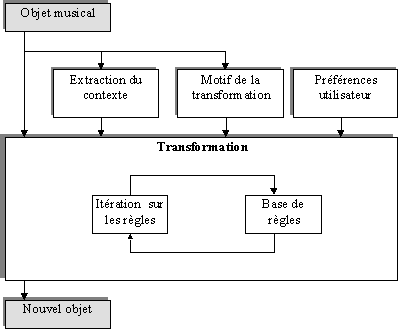
Cependant, le problème spécifique que l'on cherche à résoudre s'inscrit dans un cadre beaucoup plus général dans lequel notre solution reste valide : la résolution de la mesure de longueur non valide peut être considérée à un niveau plus global comme une transformation effectuée sur un objet musical d'OpenMusic, et guidée par des heuristiques relevant du motif pour lequel on fait cette transformation, du contexte dans lequel se situe éventuellement l'objet et de préférences propres à l'utilisateur.

IV.3 Les implications au niveau musical

Outre une réponse au problème soulevé par notre exemple précis, une telle méthodologie généralise de manière exclusive certains traitements qu'une programmation directe ne pouvait considérer que de manière incomplète. Sans qu'il soit possible de dresser une liste exhaustive, citons quand même quelques exemples d'applications directement musicales pour lesquelles la mise en ¦uvre de ce procédé trouve tout son intérêt.

 IV.3.1 Spécification par apprentissage

Les manipulations que les compositeurs effectuent pour composer leur matière sonore sont parfois très complexes et difficilement formalisables par la manière directe. La mise en ¦uvre d'un système à base de règles permet entre autres aux utilisateurs de ne définir ces nouvelles transformations qu'à partir de cas particuliers.

L'apprentissage permet de regrouper cet ensemble de décisions avec le contexte correspondant à chacune d'entre elle sous la forme de règles de réécriture. Ainsi, la nouvelle transformation réside en un ensemble de règle, dont l'observation intelligente permet la généralisation et l'exception.

IV.3.2 Aide à l'orchestration

L'exercice d'orchestration présente des similarités conceptuelles importantes avec la problématique qui nous préoccupait précédemment. En effet, distribuer une structure musicale, une progression harmonique structurée dans le temps à un groupe instrumental par exemple revient à transformer un objet musical en un nouvel objet - vraisemblablement une polyphonie - en respectant un ensemble de contraintes physiques (respect des tessitures de chaque instrument, prise en compte du jeu instrumental,... ) et de contraintes d'ordre stylistique.

 IV.3.3 Détermination automatique d'une métrique

Reporter une " valeur ajoutée " successivement de mesure en mesure pour répondre au problème de compression précédent détruit, nous l'avons vu, toute la métrique de l'objet concerné : la nouvelle métrique, dans laquelle les temps forts se retrouvent décalés, n'a plus vraiment de justification musicale. On peut donc se poser la question de savoir comment proposer une métrique pertinente pour la remplacer. De manière générale, le problème revient à proposer une métrique à un ensemble de durées successives.

Le calcul de la fonction d'autocorrélation sur un signal constitué à partir des durées successives - et éventuellement des intensités, des accentuations, qui permettent de pondérer ces durées - fournit des résultats intéressants à ce problème [Brown 93]. En particulier, on peut attendre de cet algorithme, par classement de maxima, un ensemble de signatures possibles à notre structure.

Cependant, il peut être impératif de croiser ces résultats avec des contraintes d'ordre plus musicales. De même, l'examen du contexte (une opposition binaire / ternaire par exemple) ainsi que d'éventuelles préférences du compositeur peuvent avoir toute leur importance dans ce choix. Ainsi, un système à base de règles s'applique une nouvelle fois de manière élégante à nos préoccupations.

 IV.4 Conclusion

Pour atteindre l'envergure du cas le plus général, le développement d'un tel système demande une étude minutieuse et une phase de développement et mise au point importante.

 Par exemple, le mode d'application des règles peut se faire de nombreuses manières différentes : faut-il appliquer l'ensemble des règles jusqu'à ce que plus aucune règle ne s'applique ? Que faire alors de deux règles définies par l'utilisateur de la forme : 'Si la note est un si bécarre, remplacer par un si bémol' et 'Si la note est un si bémol, remplacer par un si bécarre' ? Ne décider de n'appliquer chaque règle au maximum qu'une seule fois ? Dans quel ordre ? Pourtant certaines règles - de simplification par exemple - nécessitent d'être appliquées plusieurs fois pour aboutir au résultat attendu...

Le fait que les règles soient apprises au coup par coup ou définies par l'utilisateur impose, dans une certaine mesure, que l'ordinateur observe cet apprentissage et soit en mesure de détecter des règles contradictoires, un ensemble de règles qui, dans un enchaînement particulier deviennent contradictoires, ou encore tout simplement des règles qui ne pourront jamais s'appliquer parce que deux prédicats de leurs prémisses sont contradictoires : ces notions laissent sous-entendre l'utilisation de méta-règles, des règles donc, qui s'appliquent à des règles et en particulier à elles-mêmes.