In this section we concentrate on the relationships between the positions and the durations of activities. Imagine the composer has created a piece. S/he then wants to apply a transformation to a section of the piece. A stretch, for example. Instead of completely recalculating the structure (which may not always be possible if parts of the structure are created manually) it is advantageous to propagate the modifications incrementally. This was already expressed by Honing in his article [Hon93]:

A similar problem is encountered in the construction of graphical interfaces. Basic graphical components (buttons, text fields, icons, ...) are grouped into containers. The layout of a container depends on the locations and sizes of the components. When the container is resized (because the window is resized, for example) new locations and sizes of the components must be calculated. The graphical containers in Java's Abstract Window Toolkit (AWT) delegate the task of positioning and resizing the components to a layout manager associated to the container. Furthermore, to add a graphical component to the container a high level description of the location of the component is given instead of the precise coordinates. The insert operation is handed over to the layout manager who interprets the description and places the component at the correct location with a correct size. The model has a double advantage:

It is clear that a similar behavior is useful for time structures. We will inspire ourselves on these concepts for the organization of activities in time. Lately, we have learned that the user interface research community has since long used techniques based on local constraint propagation to specify layouts and the relations between graphical objects. Since our project was in advanced state, we leave a detailed study of these techniques for future work (the following articles can serve as a entry: [BMSX97, FB93]). More recently, these techniques have also found there entry into the realm of temporal composition of multimedia documents (see for example [FJLV98]). In the following text, we do not pretend to use techniques of logical constraint programming. However, it is in this direction that we envision our structures to evolve.

We will introduce composite structures that maintain a set of relations. The description of the relationships consists of two parts. First, we need to group all the activities that are related. Second, we need to describe the behavior of this group of activities when modifications are made. After a modification the system must verify that the relationships between the activities are still satisfied. The activities may need to be rearranged (change their start position and durations). In addition, we introduce two notions to cope with the particularities of music composition. We note:

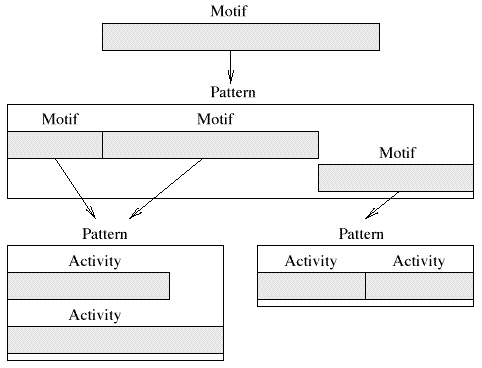
The basic element of organization is called called a pattern. The pattern holds a reference to all the participating activities and describes the relationships between them. When a modification is made to the group or to an activity, the pattern will re-organize the activities such that their internal relationships are satisfied again. A pattern has to be notified of the following modifications:

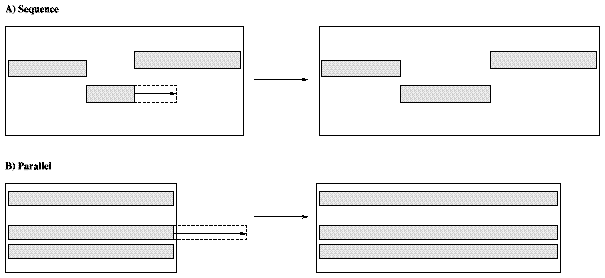
Consider the parallel and sequence organization. The sequence places the activities consecutively; the parallel organization places them simultaneously. When one of the activities changes its duration the behavior of both organizations is different. This is depicted in figure 6.2.

When we add an activity it is placed into a pattern using its start position and its duration. The definition of activities does not specify how the start position is expressed. Indeed, any type of description may do, as long as the pattern understands it. Let us give some examples. The sequence organization adds a newly inserted activity at the end of the last activity in the pattern. Similarly, the parallel organization places the activity at the start of the pattern. For both organizations, no description of the start position is needed: the position is implicit. In many music systems the start position is expressed as the exact time in seconds. In that case the description is a real value expressing the start time of the activities. However, activities can also be added with the description ``second activity.'' Or, ``the position equals twice the duration.'' It really does not matter what the description is, as long as the pattern can figure it out and put the activity in the right place. At some point the start locations of the activities must be converted into a precise time expressed in seconds. The pattern has this responsibility, since it is the only instance that knows how to deduce the exact time position. How and when this conversion takes place is discussed next.

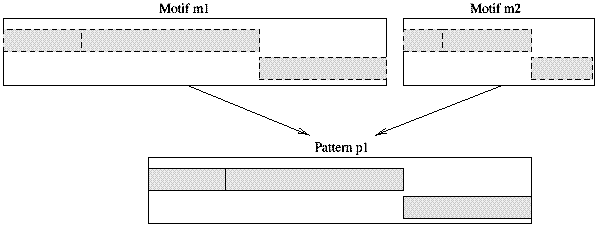
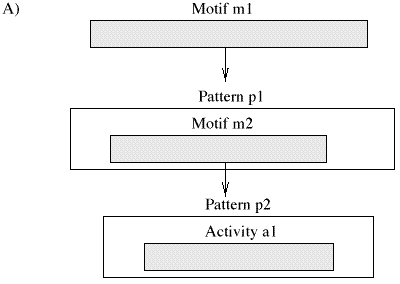
Patterns are not directly included into a music piece. There is a good reason for this. It is common in music to repeat a pattern throughout the piece. Each occurrence of the pattern might be submitted to slight variations. However, when modifications are made to the original pattern, these should be reflected by all occurrences. Buxton and colleagues already used the idea of instantiation to cope with the redundancy in music pieces [BRP⁺78]. We introduce the notion of motif. Motifs are placeholders for patterns. They are a subclass of activities and have a start location and a duration. Their contents is defined by a pattern. We will say that a motif subscribes to a particular pattern. Whenever the pattern changes, the motif is notified and can update its contents.

Figure 6.4: Several motifs can subscribe to the same pattern. The pattern clones its contained activities for each motif and organizes the activities according to the duration of the motifs.

Since a motif is also an activity, it can be included in other patterns. The described organization groups activities into patterns; motifs represent patterns as activities and can themselves be included in patterns. These structures promote an hierarchical organization of the multimedia piece in a directed graph (Fig. 6.3). Patterns, motifs, and activities interact when changes are made and when the piece is scheduled to be played. The proposed organization assures that the internal relations defining the composition are satisfied after transformations. In addition, adjustments to a structure are incremental. Motifs can also be lazy: they only request the contents of the pattern when they really need it, for example when the piece is scheduled for playback.

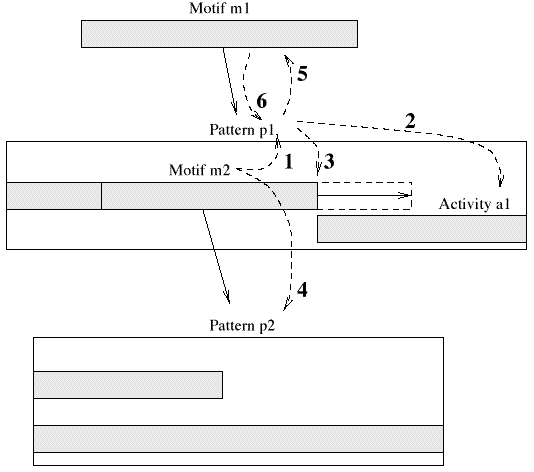
Figure 6.5: The figure shows an example of the interactions between motifs and patterns. 1) When motif m₂ is stretched it requests its container pattern p₁ to change its duration. This request may fail if the internal relations of p₁ can not be satisfied with the new duration. 2) and 3) Pattern p₁ re-organizes its contained activities: it moves activity a₁ and confirms m₂ of its new duration. 4) Motif m₂ requests its pattern p₂ to update its contents for its new duration. 5) Pattern p₁ notifies m₁ that its contents has changed. 6) Motif m₁ may react to this notiication by immediately requesting p₁ the new internal organization.

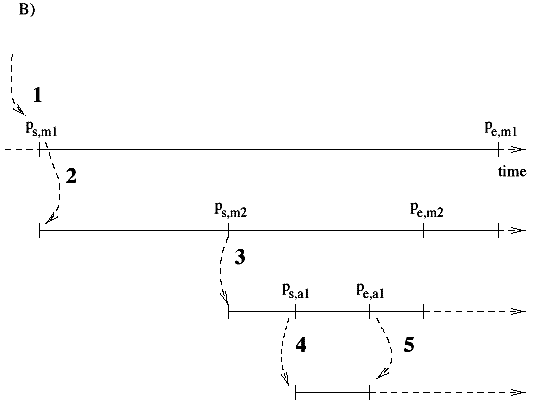
Figure 6.5 shows the interactions between the elements when the start position or duration of an activity is changed. The pattern will rearrange the activities in the group as to satisfy all the relationships. This re-organization may trickle down and affect other patterns.

Figure 6.6: Figure a) displays a simple organization of motifs, patterns, and activities. Figure B) shows the scheduling of events and the actions taken in runtime. 1) Motif m₁ schedules two events: p_s,m1 and p_e,m1. 2) m₁'s start program p_s,m1 calls pattern p₁ to schedule its activities. Pattern p₁ creates the start and end events of motif m₂. This scheduling is done in runtime. 3) The application of the program p_s,m2 provokes the scheduling of activity a₁. 4) a₁'s start program p_s,a1 creates a new synthesis process and adds it to the synthesizer. 5) a₁'s stop program p_e,a1 kills the synthesis process.

Figure 6.6 shows how the hierarchical structure of patterns and motifs is scheduled. This operation is needed when the user want to perform the piece. Since the duration of motifs are variable, the motif must request the pattern to organize its elements for the motif's duration (see Fig. 6.4). The motif ``clones'' the contained activities for the motif and gives them the appropriate start position and duration.

A piece can be scheduled dynamically or statically. When it is scheduled dynamically a motif schedules its contained activities when its start program is called. This allows late modifications to the pattern to be incorporated into the result. The disadvantage of this strategy is the application of a CPU and memory consuming scheduling task in runtime. When the structure is scheduled statically all events are created before the piece is played. This does not allow for last minute changes but is more time efficient at runtime.

The following set of Scheme procedures are some of the basic interface functions to create motifs and manipulate patterns.

With these basic functions, combined with the functions to access the member variables of activities we can easily create a set of handy functions. The procedure sequence creates a motif and sets its pattern to the sequence pattern; sequence-add adds an activity to this ``sequential motif''; stretch multiplies the duration of an activity with the given factor:

The above example adds two activities (with start at 0 and duration of 1) into the sequence. The start location of both activities is ignored by the sequence since it is defined implicitly by the pattern. The durations of the activities are scaled to the duration of the duration of the sequence (two seconds in this case). When the sequence is stretched, the contained activities are stretched accordingly.

Patterns define the organization of a set of activities; motifs reproduce a pattern in a particular context. In certain cases it can be interesting to describe ``variations'' to a pattern. We will detail this in the next section.