When working with time-based media, the composer organizes ``contents'' in time. This contents can be any time dependent data: sound, video, animation, etc ...  The contents must be played at a particular time and lasts for a certain laps of time, its duration. While composing, the composer pre-programs the system: s/he defines the time dependent contents and describes their start positions and durations. With the term activity we will indicate the description and positioning of a such a time-based contents. We will say that at some point in time the activity is triggered at which point its contents is played. This activity has a certain life span after which it ends. Two major events mark the life of an activity: the first one starts the activity, the second one ends it. The definition of an activity is as follows (we recall that V is defined as the set of anything, see section 4.3):

 

Figure 6.1: An activity is triggered by a program ps at a time position s, and ended by a program pe, d seconds later.

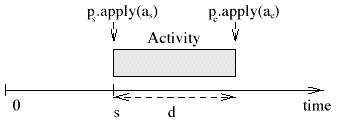
The program p_s of the activity, together with the arguments a_s describes the steps that need to be taken to start the activity. The program knows how to retrieve the contents of the activity and how to start it playing. Similarly, the program p_e and the arguments a_e describe how the activity is to be stopped (Fig. 6.1). The element s describes the start position of the activity. Note that the start position s is not necessarily expressed in a time unit for reasons that will become clear later in this chapter. Let us assume that an activity with a start position s has a start time s' expressed in seconds. To schedule an activity <s, d, p_s, a_s, p_e, a_e> two events are created and inserted in the event list of system: <s',  p_s, a_s>, and <s'+d,  p_e, a_e>.

The Activity class realized the structure described above. It is the root of most compositional elements we will discuss in this chapter. One of its principle methods is play, which will cause the evaluation of the start program and the scheduling of the stop program. The program p_s may need access to the exact start position and duration of the activity. This information is grouped in a structure called time context and will be discussed in detail further on in this text. The activity transparently inserts the time context as the first argument of the start program.

Consider for example, the activity <s, d, add, (sp), kill, (sp)> This activity, at its start time, adds the synthesis process sp to the synthesizer and kills it d seconds later. The Scheme interface defines all necessary interfaces to create activities, and set and get the fields of an activity. In our Scheme environment the activity above can be created as follows:

(define (start-sinewave context id freq amp)
  (add id (sinewave (const freq) (const amp))))

(define (stop-sinewave id)
  (kill id))

; Create a new activity starting at 0 seconds, with a duration
; of 2 seconds, that will start and stop a sinewave
(define sin-activity 
  (activity 0 2 start-sinewave '(0 440 0.1) 
                stop-sinewave '(0) ))

(play sin-activity)

In this example the start program is start-sinewave. The activity sin-activity calls this program with the additional parameters (0 440 0.1). When we look at the definition of start-sinewave, we see that the context variable has been inserted implicitly. The programs p_s and p_e of the example have a simple side effect: the addition and removal of a synthesis process. The actions taken by the programs p_s and p_e can be far more sophisticated, however. For example, they can provoke the generation and scheduling of a part of the composition. The following code is only an illustration of how more complex composition algorithms can be included. We will assume the use of a composition algorithm compose-something.

(define (compose-something context)
  ; ... insert the composition algorithm here.
) 

(define (stop-composition)
  ; ... do what ever is needed to clean up.
) 

(define piece 
  (activity 0 60 compose-something () stop-composition ()))

(play piece)

A composition comprises generally a great number of activities. It is the difficult task of the composer to specify the times, programs, and arguments of the activities. However, what intrigues both composers and music researchers most is the complex network of relationships that exists between the elements of a composition. Any of the elements of an activity <s, d, p_s, a_s, p_e, a_e> can be in complex relation to any set of elements of the other activities in the composition. The great challenge for the designer of composition environments is to provide the composer with a rich set of tools and language constructs that allow her/him to express and manipulate these multitude of relationships elegantly. In this chapter we will mainly concentrate on the time relations between the activities. In section 6.6 we consider activities that represent sound synthesis. In this case we can assume additional information on the types of arguments of the activities. We will start with the description of composite structures that maintain a set of relationships.