An accelerando is the continuous speeding up of the performance. We have discussed accelerando briefly in the discussion on time models. The following lines show how to apply a time model to a sequence of four notes. In this example we see also how breakpoint functions discussed in section 5.3.1 can be used as time models. The time model we define here is the one depicted in figure 1.7 earlier on.

(define s (sequence 2))
(sequence-add (note 0 1 vibra-voice 6000 -10))
(sequence-add (note 0 1 vibra-voice 6200 -10))
(sequence-add (note 0 1 vibra-voice 6500 -10))
(sequence-add (note 0 1 vibra-voice 6400 -10))

(define t (bpf 1 '((0 0) (0.1 0.19) (0.2 0.34) (0.3 0.46) 
                   (0.4 0.57) (0.5 0.66) (0.6 0.74) (0.7 0.82) 
                   (0.8 0.88) (0.9 0.94) (1.0 1.0))))

(set-time-model! s t)

(play s)

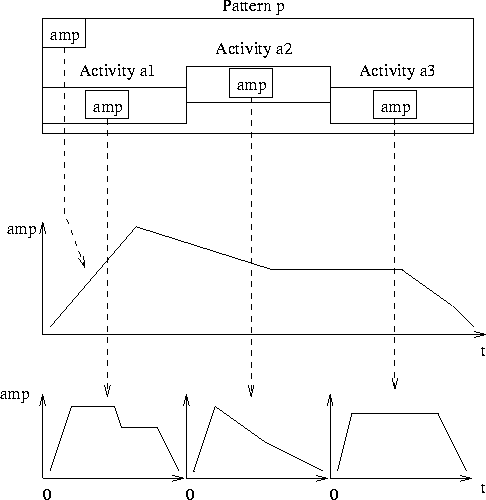
We can apply a time manipulation, such as a stretch, to the sequence defined above. Since the time-model does not depend on the duration of the motif, the contained notes are spread correctly over the length of the sequence.

In music, it is common to indicate an evolution of the dynamics for a section in the composition. We will consider the case of a sequence of notes. Figure 1.13 displays a pattern pwith three sound activities a₁ to a₃. Each of the activities has its local amplitude envelope. A sequence pattern implements the interface defines by PitchedSound. The user can therefore set a control function indicating the amplitude curve for the sequence. This envelope should be applied to the contained activities.

Figure 6.13: Defining an amplitude envelope for a pattern.

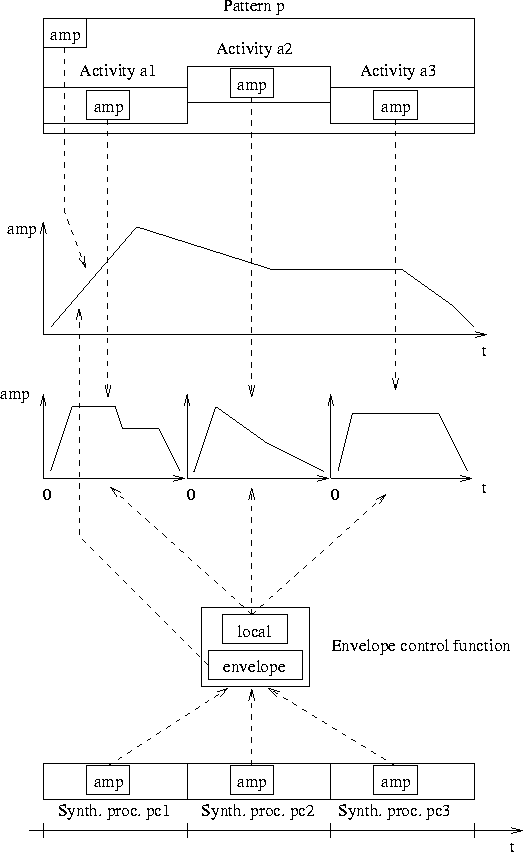
To solve this problem we define an amplitude envelope modifier and an amplitude envelope control function. The modifier is called after the pattern has organized the activities for a motif. It collects all the amplitude control functions of the individual sound activities in the pattern and replaces them with one global amplitude control function. This global control function keeps a reference to the initial control functions of the activities and to the amplitude function of the pattern. The local amplitude controllers of the activities are replaced with the global controller. When an activity a_i of the pattern is scheduled it creates a synthesis process sp_i. This synthesis process calls the global controller to obtain its amplitude value. To calculate the amplitude value the global controller first calls the initial amplitude function of the activity a_i then calls the amplitude function of the pattern p and finally multiplies the two values. Note that the values of both amplitude functions of a_i and p must be called on distinct time axes. Since the global controller receives the time context of the synthesis process sp_i as parameter, it can convert the local time of a_i to the global time of p. In this solution we retain all the initial information of the individual activities. Inspection of the control functions and modifications at runtime are still possible.

Figure 6.14: The amplitude envelope modifier.

The following lines of Scheme code shows how to create and insert an amplitude modifier into the sequence used earlier on:

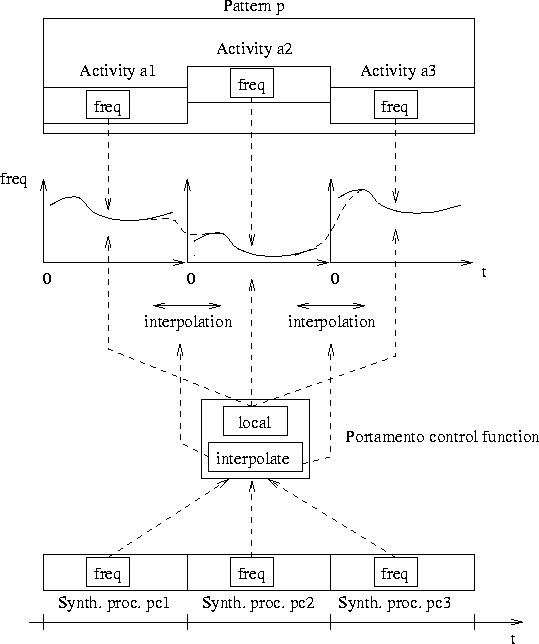
(define envelop (bpf 1 '((0 0) (0.25 1) (0.75 1) (1 0))))
(set-amp! s envelop)
(motif-set-modifier! s (amplitude-modifier))

6.7.3 Portamento and vibrato

A similar problem is portamento: a melody of notes with distinct pitches is performed in one continuous gesture. The rupture in pitch between two consecutive notes is smoothened: one note is ``carried'' to the next one. We solve this problem with the portamento modifier and the portamento control function (Fig. 6.15). The portamento modifier collects the frequency control functions of the individual activities in the pattern and replaces them with a new portamento control function. This control function returns the value of the activity's frequency control function, or an interpolated value on the edges between two activities.

Figure 6.15: The portamento modifier.

The Scheme expression to realize the portamento is as follows:

(motif-set-modifier! s (portamento-modifier))

Vibrato is the modulation of the pitch. The vibrato in a performance is, in general, coherent over a section over the music. The modulation is continuous when the performer moves from one note to the other. Furthermore, the rate of the modulation is independent from other time variations such as accelerando, etc... The vibrato in the following example is characterized by a constant frequency (in Hertz) and amplitude (as a percentage of the initial frequency). To apply a vibrato modifier to the sequence, the next line of code is entered:

(motif-set-modifier! s (vibrato-modifier 6.0 0.02))

Of course, the amplitude envelopes and the portamento scale accordingly when an accelerando time model is set for the pattern.