Oscillateur numérique

 La manipulation pratique des signaux musicaux conduit souvent à représenter les signaux dans leur zone de stabilité comme une somme pondérée de signaux harmoniques. C'est le principe de l'analyse harmonique  et des premiers types de modèles de synthèse musicale, dites de synthèse additive, utilisés dès le début des années 60.

D'un point de vue pratique, cela amène les ingénieurs à étudier et à réaliser un élément fondamental: l'oscillateur  . D'un point de vue externe (fig. 1), il s'agit d'un composant contrôlé par deux paramètres principaux: la période d'oscillation et l'amplitude d'oscillation ainsi par un paramètre auxilliaire: la phase initiale (offset de phase) . La réalisation la plus efficace et la plus simple de ce système fait intervenir dans l'équation d'évolution du système un état interne, , dit de phase courante ou d'index de phase.

Si le calcul du sinus n'est pas optimisé, cette réalisation reste trop coûteuse pour être utilisable. On gagne énormément à précalculer  le sinus dans une table d'onde  et à consulter systématiquement la table d'onde au lieu de calculer explicitement la fonction sinus à chaque échantillon. Dans ce cas, les équations d'évolution du système sont décrites par l'algorithme suivant, où f est la fonction qui permet d'accéder à la table d'onde, TableSize est la taille de la table d'onde, Step, Amp et Offset sont les paramètres de contrôle et Index l'état interne du système.

  
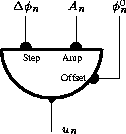
Figure 1: Schéma d'un oscillateur

,

Détermination à partir de la valeur de Index et celle de Offset du défaut d'index et des index entiers , , ... pour la réalisation de l'interpolation sur p points,

Interpolation à partir de , , ... et . Postmultiplication par Amp.

La table d'onde correspond à l'échantillonage d'une période d'onde élementaire. Il n'est pas nécéssaire de se restreindre à une table d'onde sinusoïdale. Toute forme d'onde peut a priori être utilisée. Toutefois la table d'onde est censée reproduire une période d'un signal périodique continu quelconque, donc il faut que le début et la fin de la forme d'onde coïncident afin que la continuité du signal généré soit préservée. En pratique, les formes d'ondes couramment utilisées sont les triangles, les carrés, les dents de scies, les crénaux et les sinusoïdes.

Ici l'interpolation  a pour fonction de reconstruire le signal continu à partir de sa version échantillonnée, c'est à dire un rôle de conversion numérique-analogique. Les mêmes choix technologiques qu'en conversion numérique-analogique se présentent afin d'améliorer la qualité de la synthèse: soit on augmente la résolution de la synthèse en utilisant des interpolateurs d'ordre croissant (pas d'interpolation, interpolation linéaire, quadratique ou cubique), ce qui correspond exactement à des bloqueurs d'ordre croissant (0, 1, 2, 3), soit on sur-échantillonne  la table d'onde d'un facteur 2, 4 ou 8. Le second choix est le plus souvent préféré, parce que à performances égales moins cher à réaliser.