Since the discrete version of a continuous-time delay filter is an
ideal fractional delay whose transfer function is 
, d being
a noninteger delay
, we may
consider the discrete-time system of Fig. 4 as an
intuitive counterpart of the continuous-time system of
Fig. 3. But the instantaneous feedback loop is not
realizable [3], so we propose the implementation described
in Fig. 5.
Figure 4: Nonrealisable ideal discretization
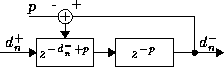
Figure 5: Realisable ideal discretization
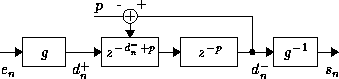
Figure 6: Complete discrete-time nonlinear one-way propagation
model of the waveguide
Then the ideal complete discrete-time model of
Fig. 6 implements the model of a time-varying
propagation speed in waveguide, and replaces the classical digital
delay-line used for constant propagation speed waveguide. The
integer parameter p can be set freely but must be greater than one.
Ideal fractional delay filters may be approached by different digital filters and different structures [4]. Because of the feedback loop, we need a particularly stable implementation for the fractional time-varying delay filter. That is why we have focused mainly on FIR implementations, and more particularly on Lagrange Interpolator Filters (LIFs).
LIFs approximate the ideal fractional delay filters at low frequency, and the valid frequency range increases with the LIF order [1]. However in our case, it appears that orders greater than 2 do not significantly improve the frequency response.
Since the original continuous-time system is nonlinear, aliasing effects may appear due to the high-frequency component generation. This component generation being intrinsic to the original system, it seems difficult to derive a theoretical dicrete-time equivalent which insures a band-limited output for any band-limited input. Therefore, for pragmatical reasons, whenever aliasing occurs, we suggest to oversample the filter, to limit the negative slope of the input signal or to introduce a low-pass filter in the feedback loop.