A.1 – CURRICULUM VITAE
Nom : ANDREATTA Prénom : Moreno Nationalité : Italienne Date et lieu de naissance : 28.04.1971 Schaffhausen (Suisse) Adresse en Italie : I-38043, Piazze di Bedollo (Trento) Adresse en France : 4, rue Charles Lebeau, 92160 Antony Adresse professionnel : IRCAM, 1 Place I. Stravinsky, 75004 Paris – Tél. : 01 44 78 16 49 Mail : Moreno.Andreatta[at]ircam.fr
Études musicales et scientifiques :
Diplômes :
Bourses et prix :
Formations :
A.2 – RECHERCHE SCIENTIFIQUE
L’activité de recherche menée à partir de ma titularisation (octobre 2005) a été envisagée selon une double perspective. D’un côté, comme le prolongement d’une activité de recherche en cours depuis la fin de la thèse et réorientée à partir d’octobre 2004 selon les grandes lignes contenues dans le projet MISA retenu par le CNRS (cf. infra) ; d’autre part, comme un moment précieux pour la mise en place d’actions spécifiques nouvelles en ce qui concerne le processus d’" institutionnalisation " du rapport mathématiques/musique en tant que discipline. Parmi ces actions, on citera, en particulier, l’organisation de séminaires d’études (MaMuX et mamuphi), le lancement de deux collections dédiées aux rapports entre sciences et musique (Collection " Musique/Sciences ", Ircam/Delatour France et " Computational Music Science ", Springer), la participation à la création d’une revue de mathématiques à comité de lecture sur les liens mathématiques/musique (Journal of Mathematics and Music) et d’une société savante (Society of Mathematics and Computation in Music) dont je suis à présent le vice-président. Dans ce rapport j’aborderai en détail uniquement l’activité de recherche, mentionnant brièvement ce deuxième aspect dans la section A.2.2.
A.2.1 L’activité de recherche sur les méthodes algébriques en musicologie computationnelle
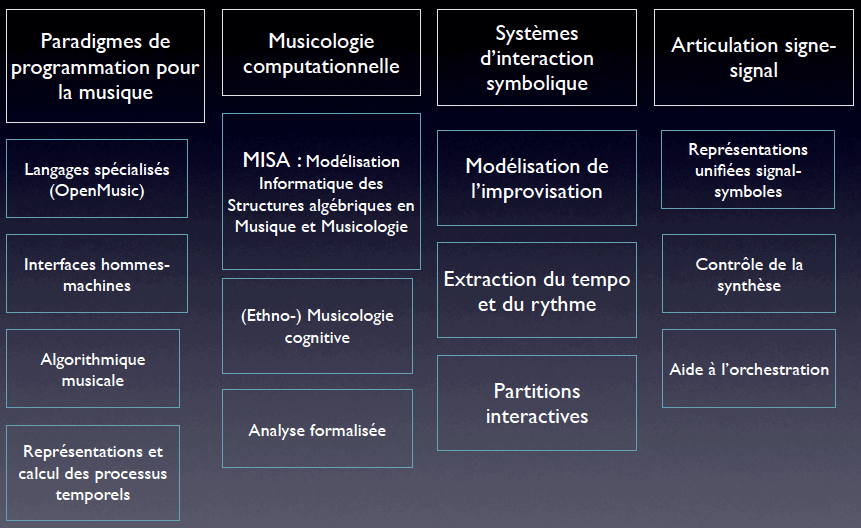
Cette recherche s’inscrit dans le projet plus général qui a été retenu par le CNRS et qui s’intitule " Modélisation Informatique des Structures Algébriques en musique et musicologie : aspects cognitifs, philosophiques et épistémologiques " (en abrégé : MISA). Le projet MISA s’inscrit formellement dans l’axe thématique " Musicologie computationnelle ", comme le montre l’organigramme suivant détaillant les domaines de recherche de l’équipe Représentations Musicales de l’Ircam (Fig. 1).

Fig. 1 : Positionnement du projet MISA dans l’organigramme des activités de recherche de l’équipe Représentations Musicales de l’Ircam (responsable : Gérard Assayag)
Avec l’objectif, à long terme, d’arriver à aborder le problème du rapport entre mathématiques, musique et sciences cognitives, tout en proposant également une nouvelle perspective philosophique couplée d’une réflexion épistémologique sur l’application des modèles algébriques en musique, j’ai concentré mon activité de recherche dans les quatre dernières années sur trois domaines en particulier que j’ai abordés à la fois d’un point de vue mathématique et informatique [1].
a) Set Theory et théories transformationnelles revisitées à travers l’approche algébrique
Le travail de généralisation de la Set Theory et de la théorie transformationnelle à travers l’approche algébrique a été mené en collaboration étroite avec des mathématiciens, tels Guerino Mazzola (MultiMedia Lab de Zürich / Université de Minnesota), Emmanuel Amiot (Professeur CPGE à Perpignan), Franck Jedrzejewski (CEA-Saclay), Thomas Noll (professeur de théorie de la musique à l’ESMuC de Barcelone et éditeur du Journal of Mathematics and Music) ainsi que des informaticiens, en particulier de l’équipe Représentations Musicales de l’Ircam. L’équipe Représentations Musicales de l’Ircam, dirigée par Gérard Assayag, est spécialisée dans l’étude des représentations symboliques de structures musicales et à leurs applications en composition assistée par ordinateur (CAO) et en musicologie computationnelle (théories et analyse musicales à support informatique). Le travail de l’équipe se fondant sur une activité de recherche et de développement dans le domaine des langages et paradigmes informatiques adaptés à la musique, je me suis tout d’abord intéressé aux aspects computationnels de la Set Theory d’Allen Forte et de la Transformational Theory de David Lewin. Pour la première, j’ai donné une formalisation " paradigmatique " (au sens de la théorie des actions des groupes) qui a été également intégrée, en collaboration avec Carlos Agon, à l’environnement informatique OpenMusic (le langage de programmation visuelle développé par l’équipe Représentations musicales) tandis que pour la deuxième j’ai proposé, avec Guerino Mazzola, une présentation " catégorielle " (au sens de la théorie mathématique des catégories) qui donne un résultat nouveau en ce qui concerne l’énumération de certaines structures globales (les " réseaux de Klumpenhouwer ") en relation d’" isographie forte ". Il s’agit d’un résultat qui ouvre des perspectives computationnelles tout à fait nouvelles pour l’analyse musicale assistée par ordinateur (cf. section B – OBJECTIFS).
D’un point de vue musicologique, les outils de représentations et de modélisation informatique permettent une approche véritablement expérimentale qui dynamise de manière significative la discipline. Ainsi des hypothèses peuvent être testées et validées en s’appuyant sur la puissance de calcul symbolique et combinatoire. D’un point de vue plus informatique, les modèles computationnels, dotés d’une certaine généricité, visent l’élaboration de langages (langages visuels, langages multi-paradigmes incluant les aspects fonctionnels, objet et logiques) et d’architectures (architectures à composants, environnement mixtes de programmation et d’édition visuelle de données). Les modèles musicaux visent à définir des représentations et des algorithmes susceptibles de capturer des aspects importants du phénomène musical. Dans le cas de la Set Theory et des théories transformationnelles, ces aspects concernent surtout l’organisation des hauteurs dans l’espace tempéré, leur représentation et leur classification. Afin d’énumérer et classer ces structures musicales, nous avons choisi une approche " paradigmatique ".
A la différence des présentations traditionnelles de la Set Theory, comme celle d’Allen Forte, de John Rahn ou de Robert Morris, la théorie des ensembles de classes de hauteurs se prête très bien à être intégrée dans une approche algébrique qui utilise pleinement la puissance combinatoire de la structure de groupe cyclique sous-jacente à toute division de l’octave musicale en un nombre n de parties égales. L’implémentation, réalisée en OpenMusic, se déploie dans une architecture " paradigmatique " basée sur l’action de certains groupes sur l’espace tempéré (le groupe cyclique en tant qu’ensemble dépourvu de structure algébrique). L’implémentation permet à l’analyste de choisir son propre critère d’équivalence entre structures d’accords en utilisant comme " paradigmes " d’analyse les différents groupes que l’on peut choisir de faire opérer sur l’espace musical. En particulier, nous avons implémenté les relations d’équivalence (donc les catalogues d’accords) induites par l’action de quatre groupes sur un tempérament musical choisi : le groupe cyclique (ou paradigme de l’équivalence à une transposition musicale près), le groupe diédral (paradigme de la Set Theory, i.e. équivalence à une transposition et/ou une inversion musicale près), le groupe affine (équivalence à une multiplication ou application affine près) et groupe symétrique (équivalence à une permutation près). L’architecture paradigmatique de cet environnement est décrite dans la figure suivante (Fig. 2) qui montre les représentations circulaires et les structures intervalliques associées aux différentes classes d’équivalence d’un même accord.
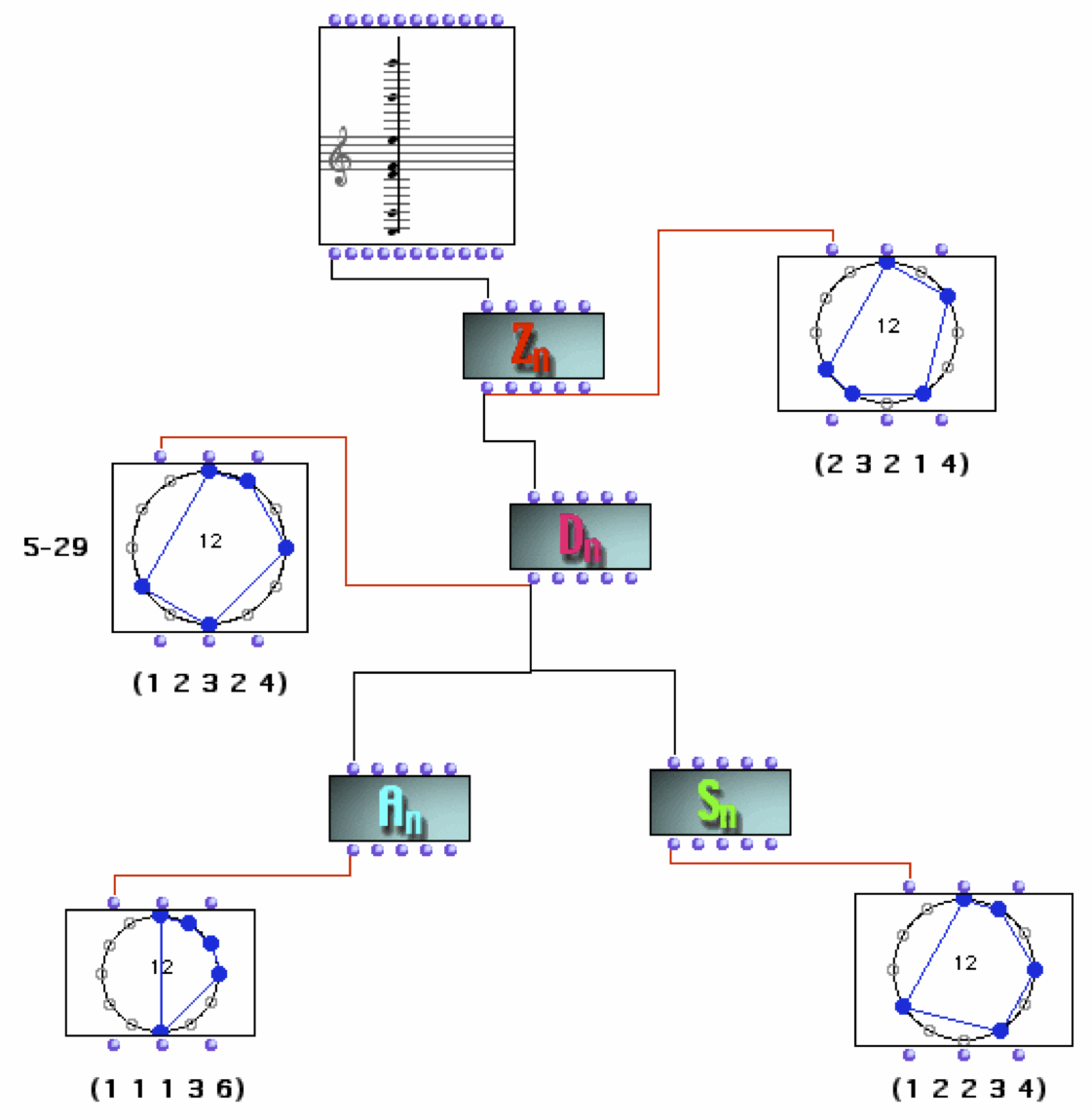
Fig. 2 : Architecture " paradigmatique " pour la théorie, l’analyse et la composition assistées par ordinateur basée sur le concept d’action d’un groupe (cyclique, diédral, affine et symétrique) sur un tempérament égal donné.
Le terme " paradigmatique " a été choisi pour souligner la portée philosophique de l’approche algébrique en analyse musicale. Les groupes algébriques jouent le rôle des " paradigmes " dans un sens très proche à celui utilisé par Thomas Kuhn dans son analyse de la structure des révolutions scientifiques. L’idée sous-jacente est celle de l’intérêt, pour un analyste ou un musicologue, de choisir le " paradigme " le mieux approprié pour décrire de façon pertinente un phénomène musical observé. Par exemple, dans l’analyse de la musique tonale, le " paradigme " du groupe cyclique (équivalence à une transposition près) sera sans doute plus pertinent du paradigme du groupe diédral (utilisé avec succès dans l’analyse de la musique atonale) ou du groupe affine (qui semble le mieux approprié pour aborder des techniques musicales typiques du répertoire jazz, comme, par exemple, la substitution d’accords). Le terme " paradigmatique " avait également été adopté en musicologie par Nicolas Ruwet dans son approche structuraliste de l’analyse musicale fortement influencé par la linguistique. Notre approche " paradigmatique ", basé sur la théorie des groupes de transformations, suggère une nouvelle interprétation de la démarche structurale en analyse musicale, indépendamment de toute considération sur le rapport entre musique et langage (cf. infra).
La démarche algébrique permet d’introduire également les concepts de base de l’analyse transformationnelle, telle que David Lewin l’a conçue à partir notamment d’une mathématisation des outils de base de la Set Theory. À la différence de l’approche " set-théorique " classique, l’analyse transformationnelle consiste à segmenter une partition de musique à travers un recouvrement de sous-ensembles qui sont liés par des opérations musicales de transposition et d’inversion. Elle permet ainsi de créer un espace abstrait de relations de transposition et d’inversion entre les accords qui peut décrire le déroulement temporel de la pièce (progression transformationnelle) ou bien une organisation spatiale des transformations algébrico/musicales (réseau transformationnel). La figure suivante (Fig. 3) montre un exemple d’une démarche transformationnelle dans le cas de l’analyse du Klavierstück III de K. Stockhausen par David Lewin [2], une analyse qui est ici reprise en utilisant la représentation circulaire pour mettre en évidence les transformations musicales qui permettent de décrire la partition à partir d’une même structure de pentacorde. Ces transformations ne changent pas la nature " ensembliste " du pentacorde, car les cinq formes sont " équivalentes " à une transposition ou une inversion près (ou une combinaison des deux opérations).
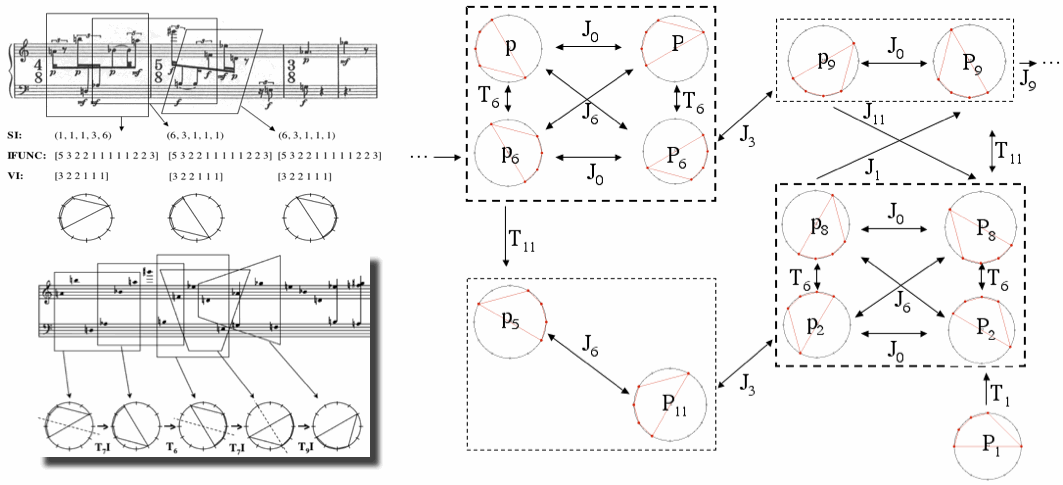
Fig. 3 : Segmentation par imbrication et progression/réseau transformationnels associés à l’aide de la représentation circulaire.
J’ai également entrepris un travail de généralisation de la Set Theory et de l’analyse transformationnelle via la théorie des catégories, une approche qui n’avait pas pu être approfondie pendant la thèse de doctorat et dont l’intérêt à la fois mathématique et musical est au cœur du projet MISA. Ce travail, mené en collaboration avec le mathématicien Guerino Mazzola, est décrit dans un article qui montre que les réseaux de Klumpenhouwer, outil très sophistiqué de la théorie transformationnelle américaine, sont en réalité des exemples de " limite ", au sens de la théorie des catégories [3]. La figure suivante (Fig. 4) montre un exemple d’utilisation des réseaux de Klumpenhouwer (K-net ou K-réseau) et leur caractère récursif.
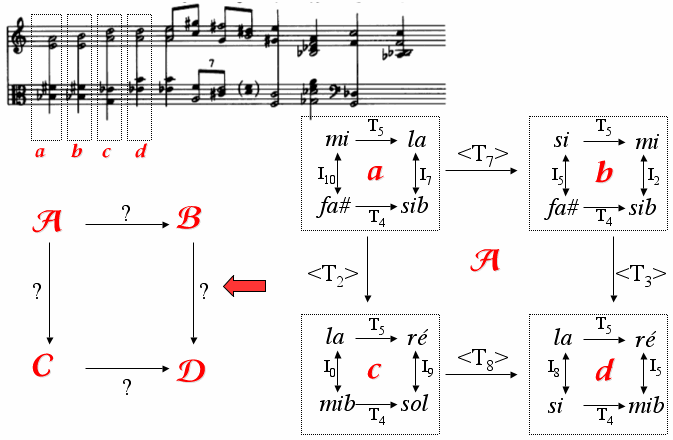
Figure 4. Un exemple de réseaux de Klumpenhouwer, configurations spatiales diagrammatiques déployant des transformations de transpositions et d’inversions, et de leur récursivité.
En étudiant la structure des K-réseaux comme une catégorie (cette des graphes dirigés), on peut étudier d’un point de vue catégoriel les isomorphismes entre deux K-reseaux ainsi que les principes récursifs permettant de construire un réseau de réseaux de réseaux et ainsi de suite.
La formalisation catégorielle des K-réseaux a deux grands avantages. D’un côté elle permet de donner un résultat d’énumération des K-réseaux en relation d’isographie forte (strong isography), c’est-à-dire ayant la même configuration de flèches. D’autre part elle intègre, de par sa nature même, le principe de récursivité. La famille des réseaux en relation d’isographie forte avec un K-réseau donné est isomorphe à un sous-groupe du groupe (Z/nZ)m ou m est le nombre des sommets du graphe. La figure suivante (Fig. 5) donne, par exemple, les quatre K-réseaux en relation d’isographie forte, un résultat qui découle directement de la notion de limite d’un diagramme.
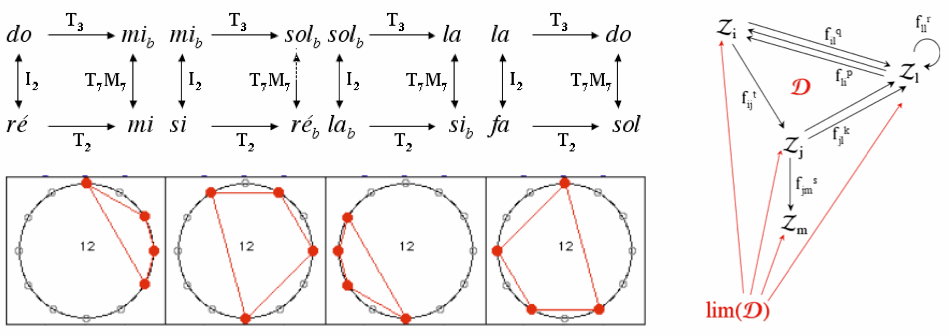
Fig. 5 : Quatre réseaux en relation d’isographie forte (Tk, Ih et Ms indiquant les opérations de transposition, inversion, et application affine) et limite d’un diagramme catégoriel.
D’autre part, il est tout a fait naturel d’abstraire chacun des réseaux précédents et les transformer dans des sommets d’un potentiel réseau de réseaux, ayant comme flèches des transformations isographiques (dans ce cas l’identité) entre des réseaux sous-jacents. La construction s’applique dans des cas beaucoup plus généraux de façon tout à fait naturelle, car l’un des avantages de la théorie des catégories est précisément de pouvoir construire des transformations entre catégories (foncteurs) ainsi que des transformations entre foncteurs (transformations naturelles). Cette démarche ouvre la voie à une théorie nouvelle des " gestes ", que nous avons esquissée (de façon conjecturale) dans un article publié dans le premier numéro du Journal of Mathematics and Music [4] et dont la formalisation précise et l’étude des ramifications philosophiques et retombées cognitives constitue l’un des objectifs des quatre prochaines années.
J’ai commencé à aborder les enjeux d’une démarche structurale en musique et musicologie du XXe siècle lors d’une journée scientifique du Centre Georges Canguilhem (2 décembre 2004) intitulée " Les structures après le structuralisme " (organisée par Frédéric Patras, Laboratoire J. A. Dieudonné, Université Sophia Antipolis, Nice). J’ai ensuite discuté les ramifications philosophiques et épistémologiques de la tradition set-théorique et transformationnelle en analyse musicale lors d’une série d’interventions dans le cadre du séminaire " Mathématiques/Musique & Philosophie " de l’ENS (18 novembre 2006, 6 octobre 2007 et 16 janvier 2010). En particulier, dans la première intervention intitulée " Mathématiques, musique et philosophie dans la tradition américaine : la filiation Babbitt/Lewin [5]", j’ai présenté quelques aspects théoriques et métathéoriques de la tradition américaine (du sérialisme intégral de Milton Babbitt aux réseaux transformationnels d’Henry Klumpenhouwer) en essayant d’en discuter les hypothèses épistémologiques sous-jacentes et les implications philosophiques qui dérivent d’une telle démarche, aussi bien pour la théorie que pour l’analyse musicale. Nous avons pu montrer l’influence directe du positivisme logique, et en particulier le Cercle de Vienne, dans l’émergence d’un paradigme mathématique en théorie de la musique aux Etats-Unis, comme le confirme une analyse comparée des principes des bases des deux courants de pensée. Cependant, on peut montrer comment la réflexion théorique de Milton Babbitt ainsi que la démarche transformationnelle de David Lewin dépassent largement le paradigme langagier qui sous-tend le positivisme logique et engagent d’autres formes de relations entre la musique et les mathématiques. Nous avons esquissé en conclusion les principes de base d’une interprétation de l’analyse transformationnelle et, en particulier, des réseaux de Klumpenhouwer (K-nets) à l’aide de la théorie des catégories et des topoï ainsi que les conséquences théoriques et philosophiques d’une telle formalisation. Dans la dernière intervention au séminaire mamuphi (16 janvier 2010), nous sommes revenus sur les implications philosophiques d’une démarche transformationnelle en théorie et analyse musicales. Bien qu’ayant des rapports étroits avec le positivisme logique, nous proposons une nouvelle lecture philosophique de l’approche transformationnelle visant à élargir les catégories structurales appliquées traditionnellement à la musique more linguistico afin de mettre en lumière des nouveaux enjeux philosophiques relevant du rapport entre structuralisme et phénoménologie.
L’objectif futur est d’arriver à une formulation précise du cadre philosophique et épistémologique sous-jacent à une approche algébrique en théorie, analyse et composition musicales, avec une étude des retombées cognitives des modèles algébriques et catégorielles en musique.
Direction de travaux d’étudiants sur ce sujet :
b) La construction des mosaïques et des pavages en théorie et composition musicales
Le problème de la construction de canons musicaux rythmiques réalisant un pavage de l’axe du temps a été à l’origine de mon intérêt pour le domaine des relations entre mathématiques et musique. Ce problème musical, dont j’avais commencé l’étude algébrique dans ma tesi di laurea [7] a donné lieu à de nombreux résultats et constitue l’un des axes de recherches autour duquel nous avons su fédérer une communauté de mathématiciens, informaticiens, théoriciens de la musique et compositeurs [8]. Musicalement il s’agit de construire un canon rythmique, i.e. une forme musicale obtenue par translation temporelle d’un pattern rythmique, ayant la propriété de réaliser un pavage de l’axe du temps. Le pattern rythmique, translaté d’un nombre fini de fois, pave l’axe des entiers de telle façon que chaque instant du temps est rempli par une (et une seule) pulsation du rythme de base. Le mathématicien Dan Vuza a proposé un modèle de canon rythmique réalisant un pavage de l’axe du temps obtenu par factorisation d’un groupe cyclique en somme directe de deux sous-ensembles non-périodiques (que l’on a appelé par la suite " Canon de Vuza "). Notre recherche a été d’abord de replacer ce problème dans le cadre de la théorie des groupes de Hajos ou good groups, i.e. les groupes pour lesquels pour toute factorisation en somme directe de k sous ensembles, au moins l’un de ces sous ensembles est périodique [9]. Cela nous a permis de montrer les liens entre ce problème musical et la conjecture de Minkowski sur le pavage de l’espace n-dimensionnel par des cubes unité ainsi qu’une série d’autres conjectures dont certaines sont toujours ouvertes (telles la conjecture quasi-périodique de Hajos et la conjecture spectrale de Fuglede). Nous avons ensuite abordé les aspects computationnels en étudiant l’espace combinatoire des solutions pour une période donnée (i.e. par un ordre donné du groupe cyclique sous-jacent). L’implémentation de ce modèle, ainsi que des modèles plus généraux obtenus par augmentations des voix du canon (Augmented Canons) ou par produit de polynômes cyclotomiques (Cyclotomic Canons), a été réalisée en collaboration avec Carlos Agon, chercheur au sein de l’équipe Représentations musicales et intégré dans OpenMusic (à partir de la version 5.0. Cf. Section 9. Logiciels).
Nous avons donné une classification exhaustive des solutions dans le cas de la factorisation du groupe cyclique Z/72Z en deux sous-ensembles non périodiques, cet ordre étant le plus petit pour un groupe n’ayant pas la propriété de Hajos. Cette classification a été établie en suivant une approche " paradigmatique ", i.e. basée sur l’utilisation de plusieurs groupes dont l’action sur les sous-ensembles R et S d’une factorisation permet de réduire de façon structurelle le catalogue des solutions. En particulier cette approche tient compte de l’action de trois groupes différents sur le groupe cyclique d’ordre 72, considéré en tant qu’ensemble : le groupe cyclique, le groupe diédral et le groupe affine. Le résultat surprenant que nous avons obtenu concerne la réduction du catalogue des solutions à deux seuls canons rythmiques mosaïques à une application affine près (Fig. 6).
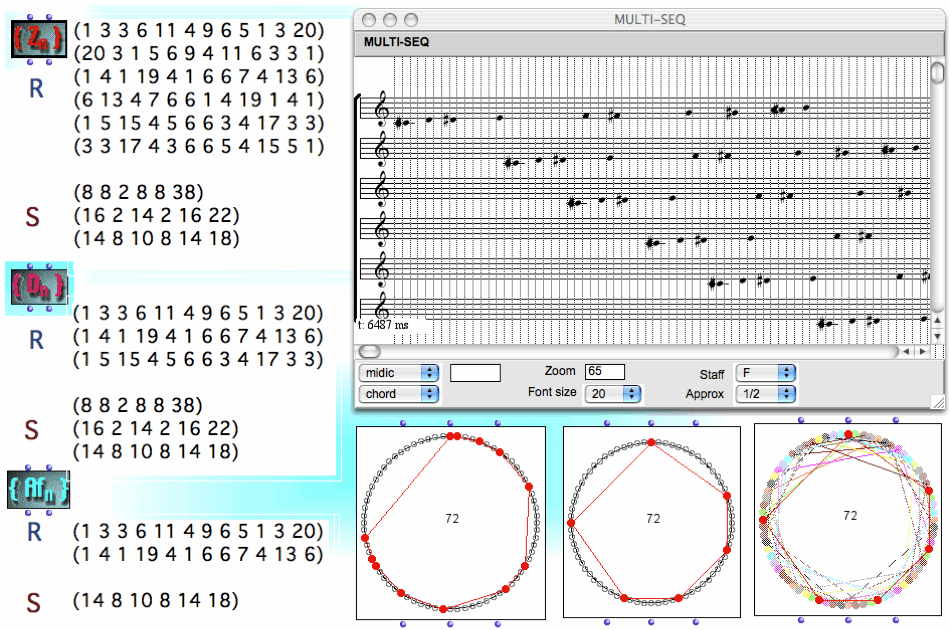
Fig. 6 : Classification " paradigmatique " des canons mosaïques de Vuza d’ordre 72 (par rapport à l’action du groupe cyclique, diédral et affine). L’action du groupe symétrique ne peut pas être utilisé car elle détruit la structure de canon.
Les canons de Vuza représentent des objets mathématiques remarquables car ils sont la clé pour la résolution de la conjecture de Fuglede ou conjecture spectrale. Cette conjecture affirme qu’un domaine de l’espace euclidien n-dimensionnel admet un spectre ssi il pave Rn par translation. Sans perte de généralité, on peut tout d’abord se réduire au cas du pavage de l’axe des réels au pavage du groupe cyclique Z/nZ. On peut ensuite montrer que s’il existe un sous-ensemble R de Z/nZ qui pave le groupe cyclique d’ordre n sans être spectral, alors R est essentiellement le rythme de base d’un canon de Vuza. D’où l’intérêt d’avoir une classification exhaustive des canons de toute factorisation d’un groupe cyclique non-Hajos en somme directe de deux sous-ensembles non-périodiques. Nous avons consacré un numéro spécial du Journal of Mathematics and Music (guest editors : Moreno Andreatta et Carlos Agon, Mai 2009) aux rapports entre la construction des canons rythmiques mosaïques et la conjecture spectrale.
D’un point de vue musical, ce travail a fourni le modèle formel pour plusieurs compositions. Le travail mené avec le compositeur Georges Bloch, par exemple, est emblématique en ce qui concerne les directions parfois très inattendues qu’une recherche théorique peut prendre lorsqu’elle est soumise à la singularité de la pensée compositionnelle. Les enjeux de cette collaboration interdisciplinaire ont été présentés et discutés en détail lors d’un Workshop qui s’est déroulé à Dublin sous invitation de l’association Seed " Art & Science " et organisé sous l’égide de la Irish Royal Academy (voir liste de publications). Le problème des pavages et mosaïques en musique est sans doute l’un des axes de recherche parmi les plus actifs en théorie mathématique de la musique. L’un des objectifs des prochaines années sera d’impliquer un nombre croissant de mathématiciens travaillant sur le problème de la factorisation de groupes finis afin d’essayer d’apporter quelques résultats nouveaux en direction de la solution de la conjecture spectrale.
Direction de travaux d’étudiants sur ce sujet :
c) La relation Z en musique, la DFT et la théorie des ensembles homométriques
En travaillant sur certains aspects combinatoires des structures musicales, plusieurs compositeurs et théoriciens de la musique ont essayé d’établir les bons invariants par rapport au problème de la classification " paradigmatique " (dans le sens de l’utilisation de l’action de différents groupes sur l’ensemble des parties d’un groupe cyclique Z/nZ et de la relation d’équivalence qu’en découle).
Dans le problème de la classification d’accords modulo l’action du groupe diédral, l’outil de base est ce qu’on appelle le " contenu intervallique ". Etant donné un accord A ={0, a1, a2, … ak}, son contenu intervallique (indiqué par CI) est le multiset CI(A)= [b0, b1, …, b11] dans lequel l’élément bi indique combien de fois l’intervalle de i demi-tons est contenu dans l’accord. Le contenu intervallique compte ainsi le nombre d’occurrences de chaque intervalle (de 0 jusqu’à 11) dans un accord. Le contenu intervallique s’exprime comme produit de convolution de fonctions caractéristiques: CI(A)=1A*1-A.
Le contenu intervallique n’est pas un invariant dans le problème de la classification d’orbites par rapport à l’action du groupe diédral. En effet, deux accords sont dans la même orbite auront le même contenu intervallique mais il se peut que deux accords aient le même CI sans être dans la même orbite. C’est ce qu’on appelle la relation Z que l’on indiquera avec ~Z. On peut montrer que relation Z est en réalité un cas particulier de la théorie des ensembles homométriques [10]. De plus, en introduisant la transformé de Fourier discrète (DFT) d’un sous-ensemble d’un groupe cyclique Z/nZ, on arrive à une formalisation élégante de la relation Z (et donc des ensembles homométriques). Etant donné deux sous-ensembles A et B de Z/nZ, A~ZB ssi les modules de la DFT de A et B coïncident. Ceci ouvre la question de la récupération de la phase (phase retrieval) en théorie mathématique de la musique, autrement dit comment reconstruire une structure musicale (accord, pattern rythmique, …) à partir de son contenu intervallique. Il s’agit d’un problème qui reste ouvert, comme d’ailleurs celui d’une énumération exhaustive de toutes les parties de Z/nZ en Z relation pour un tempérament égal donné [11]. Notre contribution dans ce domaine a été surtout l’étude computationnelle de la relation Z généralisée (ou relation Zk). Par définition deux sous-ensembles A et B de Z/nZ sont en relation Zk si toute orbite de cardinalité k (par rapport à l’action du groupe diédral) est contenue le même nombre de fois dans les deux sous-ensembles. La fig. 7 montre un exemple de relation Z4 entre deux sous-ensembles du groupe cyclique d’ordre 36.
Direction de travaux d’étudiants sur ce sujet :
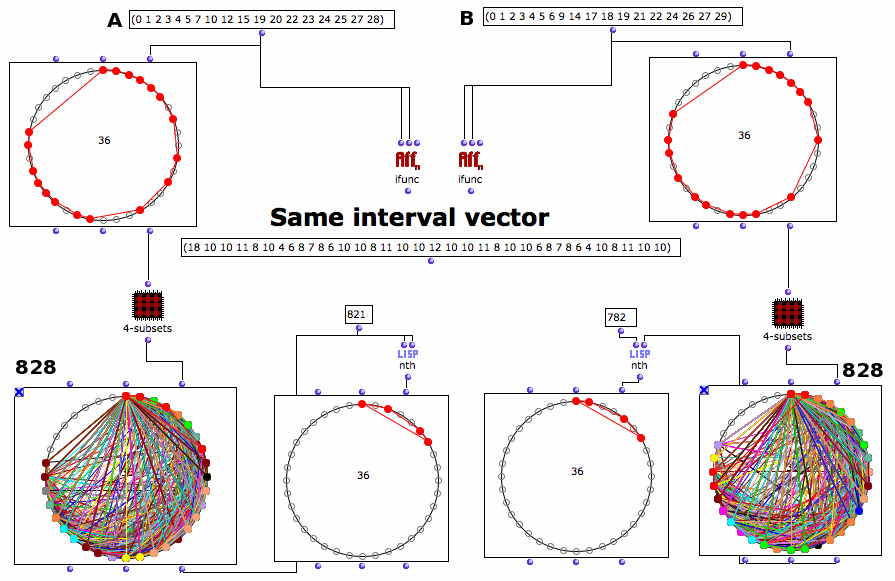
Fig. 7 : Un exemple de relation Z généralisée entre deux sous ensembles A et B du groupe cyclique d’ordre 36 dans l’implémentation que nous avons réalisée en OpenMusic (travail en cours en collaboration avec Daniele Ghisi, département de mathématique de l’université de Milano Bicocca, John Mandereau, département de mathématiques de l’université de Pisa et Carlos Agon, Ircam).
A.2.2 Valorisation et transmission des connaissances
Le domaine des rapports entre mathématiques et musique n’étant pas encore " institutionnalisé ", il m’a semblé tout à fait indispensable d’envisager des nouvelles actions visant à unifier les efforts de la communauté scientifique qui souhaite s’engager dans ce champ de recherche. Je voudrais souligner deux aspects de ce travail de valorisation : un premier aspect concernant les activités liées aux publications et un deuxième visant des actions spécifiquement pédagogiques.
a) Création d’un contexte favorable pour les publications sur mathématique/musique
Afin d’augmenter le caractère institutionnel des activités " mathémusicales ", j’ai participé au projet de création de la première revue à comité de lecture sur mathématique/musique. Cette étape, indispensable à la constitution d’une véritable communauté de chercheurs travaillant sur ce nouveau domaine, a été discutée à plusieurs reprises à l’occasion des deux dernières rencontres de l’American Mathematical Society (Phoenix, Arizona 7-10 janvier 2004 et Evanston, Illinois, 23-24 octobre 2004) auxquelles j’ai eu l’occasion de participer. L’intérêt croissant pour ce champ de recherche de la part de l’AMS, qui depuis 2003 organise des séances spéciales sur les " Méthodes Mathématiques en Analyse Musicale ", a donné un élan majeur au projet de création de la revue. Un comité éditorial a été constitué réunissant les plus grands spécialistes du domaine mathématique/musique (y compris des personnalités qui soutiennent ce projet à titre honorifique, tels Pierre Boulez en France et Milton Babbitt aux Etats-Unis). Le premier numéro du Journal of Mathematics and Music (édité par Taylor & Francis) a été présenté officiellement lors du premier Colloque International Mathematics and Computation in Music (Berlin, 18-20 mai, 2007). A cette occasion nous avons posé les bases pour la création d’une société savante, la Society of Mathematics and Computation in Music, qui se réunit tous les deux ans à l’occasion de la conférence Internationale MCM. La troisième édition des MCM sera organisée par l’équipe Représentations Musicales de l’Ircam et aura lieu pendant le Festival Agora (Juin 2011).
Une action similaire a été menée pour encourager la publication d’ouvrages sur " Mathématique/Musique " et, plus en général, sur les rapports entre la recherche musicale et l’activité scientifique. Grâce à une proposition de Jean-Michel Bardez (Président de la SFAM, Société Française d’Analyse Musicale), j’ai participé à la conception d’une nouvelle collection d’ouvrages intitulée " Musique/Sciences ". Cette collection, co-dirigée par Jean-Michel Bardez et moi-même, a été crée en coédition avec l’Ircam et les éditions Delatour France et bénéficie du soutien de la SFAM et du CNRS (UMR 9912). Elle a un caractère pluridisciplinaire et propose des ouvrages aussi bien en français, en anglais qu’en édition bilingue. Liste des 12 ouvrages déjà parus (en ordre chronologique) [12] :
J’ai également participé à la création d’une collection chez Springer (Computational Music Science), que je codirige avec Guerino Mazzola (University of Minnesota / University of Zürich). Liste d’ouvrages parus et à paraître [13] :
b) Nouvelles actions pédagogiques pour renforcer l’axe mathématique/musique
Parallèlement à l’organisation du Séminaire MaMuX (Mathématique/Musique et relations avec d’autres disciplines) de l’Ircam, j’ai également participé à la création en 2004 d’un nouveau Séminaire mamuphi (Mathématique/Musique et Philodsophie) à l’ENS, dont je partage la direction avec François Nicolas (compositeur) et Charles Alunni (philosophe et Directeur du Laboratoire Disciplinaire " Pensé des Sciences "). Nous avons également mis en place une nouvelle école de mathématiques pour musiciens et d’autres non-mathématiciens, organisée sous l’égide du Séminaire MaMuX et mamuphi et animée initialement par Yves André (ENS/CNRS) et actuellement par Pierre Cartier (IHES). Je vais décrire brièvement ces trois initiatives.
Depuis 2001 je coordonne le Séminaire MaMuX (Mathématique/Musique et relations avec d’autres disciplines) de l’IRCAM (co-organisé avec Carlos Agon). Le Séminaire de travail MaMuX, cherche à développer une hypothèse de pertinence, à la fois musicale et mathématique, du rapport mathématiques/musique à travers une exploration des liens qui se créent avec d'autres disciplines dont la philosophie, l'épistémologie, la linguistique, l'informatique et les sciences cognitives.
Les différentes séances qui ont eu lieu depuis 2001 peuvent être regroupées selon ces thèmes :
Comme je l’ai montré dans mon rapport de recherche (section A.2.1), ces axes thématiques autour desquels on a décidé d’orienter notre séminaire ont également été des catalyseurs importants dans ma propre activité de recherche (en particulier, les axes de recherche sur la Set Theory et la théorie transformationnelle et les mosaïques et pavages dans la musique). Le Séminaire MaMuX s’appuie maintenant sur une collaboration permanente avec des mathématiciens, notamment Guerino Mazzola (Université de Minnesota), Franck Jedrzejewski (CEA, Saclay), Thomas Noll (ESMuC, Barcellona) et Emmanuel Amiot [14].
Depuis 2004, et parallèlement au Séminaire MaMuX, je codirige avec François Nicolas et Charles Alunni le Séminaire " Musique et Mathématique ". Trois sujets ont été abordés jusqu’au présent dans le séminaire :
A partir de la saison 2007-2008, nous n’avons pas fixé de thématique précise pour ce séminaire qui est donc ouvert à de propositions d’interventions tout azimut sur les rapports entre mathématiques/musique et philosophe [15]. J’ai participé à ce séminaire avec plusieurs interventions consacrées aux ramifications philosophiques des modèles algébriques appliqués à la musique (voir liste des publications, section 6. Séminaires, Workshops). Un numéro spécial de la Revue de Synthèse (sous la direction de François Nicolas, Charles Alunni et moi-même) est actuellement en préparation (date prévu de publication fin 2010).
Ecole mathématique pour musiciens et d’autres non-mathématiciens
J’ai parallèlement participé, toujours avec François Nicolas et Charles Alunni, à la mise en place d’une nouvelle école qui s’inscrit formellement dans le Séminaire MaMuX mais qui est organisée en partenariat avec le Séminaire mamuphi. Le principe en est tout à fait singulier car il s'agit de rendre compréhensible un concept central de la mathématique la plus contemporaine à des non-spécialistes, en tentant de les mener au cœur de la pensée mathématique la plus active, et sans économiser ni la spécificité de l'écriture mathématique. La première saison de l’école (2006-2009) était animée par Yves André (CNRS/ENS), [16]. Depuis fin 2009 l’école est animée par Pierre Cartier (IHES).
LISTE DES PUBLICATIONS (2005-2009)
Dans le cas des revues à comité de lecture, le publications sont numérotées selon l’ordre décroissant d’importance que je leur accorde du point de vue de l’apport à mon domaine de recherche et de l’impact de mes travaux). Voir le document séparé pour la liste complète des publications.
1. Revues à comité de lecture et direction de numéros de revue
2. Conférences invitées dans des congrès
3. Actes de colloques à comité de lecture
4. Publications dans des revues sans comité et ouvrages de vulgarisation
5. Communications à des congrès, symposium (n’ayant pas donné lieu à des actes)
6. Séminaires, workshops, tutorials
7. Livres et ouvrages
8. Chapitres d’ouvrages
9. Logiciels
Conception et réalisation avec C. Agon de l’environnement MathTools en OpenMusic, le langage de programmation visuelle pour la composition assistée par ordinateur développé à l’Ircam. Ce module logiciel, disponible à partir de la version 5.0 d’OpenMusic, présente notamment pour la première fois de façon cohérente les diverses approches algébriques en ce qui concerne la construction des canons rythmiques mosaïques (Tiling rhythmic canons, voir section A.2.1 pour une description plus détaillée des aspects théoriques et informatiques liés à la construction des canons rythmiques mosaïques). L’environnement MathTools, fruit d’une collaboration avec plusieurs mathématiciens et informaticiens (dont Emmanuel Amiot, Thomas Noll, Franck Jedrzejewsky, Guerino Mazzola, Dan Tudor Vuza, …) offre également une palette d’outils destinés aux recherches autour de la théorie mathématique de la musique assistée par ordinateur. Il a été présenté dans le cadre de plusieurs conférences, Workshops et Tutorials, en particulier :
A.3 – ENSEIGNEMENT, FORMATION ET DIFFUSION DE LA CULTURE SCIENTIFIQUE
Thèses et travaux de recherche dirigés
Depuis mon entrée au CNRS j’ai assuré la direction ou co-direction d’une série de travaux universitaires, allant du mémoire de magistère en mathématiques jusqu’au mémoire pour l’obtention d’un diplôme de traduction en passant par des mémoires de master (LM2), de " tesi di laurea " et de thèse de doctorat. Voici la liste complète des activités d’encadrement :
Participation à l’enseignement
J’assure régulièrement des cours de modélisation mathématique pour l’informatique musicale dans le cadre de trois formations doctorales :
Je suis également sollicité pour des cours dans le cadre de formations musicales, aussi bien en France qu’à l’étranger. J’ai assuré, par exemple, un cours de 3h d’initiation aux rapports mathématiques/musique aux élèves du Conservatoire national supérieur de Paris (18 mars 2005), un cours de 12h annuelles sur la formalisation algébrique des structures musicales au conservatoire d’Adria, en Italie (de 2004 à 2006) et plusieurs cours d’introduction aux méthodes algébriques en musique pour les compositeurs du cursus de composition et informatique musicale de l’Ircam (durée variable). Pendant l’année 2008-2009 j’ai été Visiting Professor à l’université de Pisa (département de mathématiques) et à l’université de Milan (département d’informatique) pour deux cours sur les méthodes algébriques en musique respectivement de 30h et de 15h.
Depuis septembre 2009 je suis co-responsable, avec Mikhail Malt, des unités d’enseignement " Musique et sciences depuis 1945 (MSV) " et " Applications de l’acoustique, du traitement du signal et de l’informatique à la création musicale contemporaine (CMC) " dans le cadre de la formation ATIAM de l'Ircam, où j’assure également un cours de 6h sur la musique algorithmique.
Participation à l’organisation de conférences et de colloques (en dehors des Séminaires MaMuX et mamuphi)
Participation à des ouvrages de vulgarisation
Intervention dans la presse
Participation à des travaux d’expertise
A.4 – TRANSFERT TECHNOLOGIQUE, RELATIONS INDUSTRIELLES ET VALORISATION
Néant.
A.5 – ENCADREMENT, ANIMATION ET MANAGEMENT DE LA RECHERCHE
A.5.1 Responsable du projet " Mathématiques/Musique & Cognition " financé par l’AFIM (Association Française d’Informatique Musicale). Ce projet a déjà permis d’envisager l’un des aspects qui est resté jusqu’à présent très peu étudié dans le cadre du projet MISA, à savoir le problème des ramifications cognitives et perceptives d’une approche algébrique en musique (cf. section B - OBJECTIFS). Liste des journées d'étude et Symposia organisées dans le cadre des activités du groupe de travail [17] :
A.5.2 Responsable du projet exploratoire " Géométrie de l’Interaction et Musique " (dans le cadre des projets PEPS Interaction Math-ST2I)
Ce projet vise à étudier les champs d’applications possibles de la géométrie de l’interaction de Jean-Yves Girard à l’informatique musicale. À la différence des paradigmes de programmation traditionnels en informatique musicale (programmation logique et fonctionnelle, calcul concurrent, …), dont la composante logico/informatique prime sur les enjeux proprement mathématiques, la géométrie de l’interaction postule une primauté des constructions mathématiques (théorie des opérateurs et algèbres de von Neumann) sur la logique. Ceci pourrait avoir des conséquences importantes dans une discipline, la musique, dont on a désormais abondamment étudiés les enjeux mathématiques sans pourtant arriver à proposer des outils théoriques nouveaux pour étudier ses rapports profonds avec la logique [18]. Liste des journées d'étude organisées dans le cadre des activités du groupe de travail " Géométrie de l’interaction et musique " :
A.5.3 Soumission du Projet " MATHnMUSIC : Approaching open problems in mathematics through music ", dans le cadre des appels " Starting Grant " de l’European Research Council (en cours d’évaluation. Cf. section B - OBJECTIFS).
L’objectif le plus ambitieux pour les quatre prochaines années est celui que nous avons décrit en détail dans le projet " MATHnMUSIC ", actuellement en cours d’évaluation par l’European Research Council. Dans ce projet, nous partons du constat que nonobstant le progrès significatif dans le domaine des relations entre mathématiques et musique ainsi que la découverte d’un nombre toujours croissant de problèmes mathématiques posés par la musique, il n’existe à présent officiellement aucune équipe de recherche dédiée à la recherche " mathémusicale ". Il serait donc extrêmement crucial d’arriver à constituer un groupe de recherche ayant comme mission principale celle de faire avancer le domaine des rapports entre mathématiques et musique. Un tel groupe de recherche pourrait s’attaquer à une série de conjectures ouvertes en mathématiques à partir de problèmes posés par la théorie de la musique et la composition. Pour cette raison, il serait important qu’une telle équipe de recherche soit intégrée dans un environnement interdisciplinaire garantissant une interaction naturelle avec de musiciens et de compositeurs qui font appel à de méthodes mathématiques et à de modèles computationnels dans leur activité. En intégrant une équipe de recherche " MATHnMUSIC ", les mathématiques auraient une place naturelle à l’intérieur du spectre très large de sujets représentés à l’Ircam. De cette façon, on assisterait sans doute à une accélération importante dans le processus d’institutionnalisation de la recherche " mathémusicale " en tant que discipline académique.
Au-delà de la dimension de recherche académique, le projet " MATHnMUSIC " a des objectifs pédagogiques ambitieux, car il ouvre des horizons nouveaux pour l’enseignement des mathématiques. Pour un public de non spécialistes, notre expérience montre qu’il est tout à fait possible de rendre plus intuitifs et attrayants des concepts abstraits en les introduisant à l’aide d’idées musicales. Afin de réagir au scepticisme contemporain envers les mathématiques, il pourrait donc se révéler précieux d’approcher de concepts mathématiques à partir des constructions musicales sous-jacentes. La figure suivante (Fig. 8) détaille les objectifs à court, moyen et long terme des activités à la fois de recherche et de pédagogie en ce qui concerne les rapports mathématiques/musique.
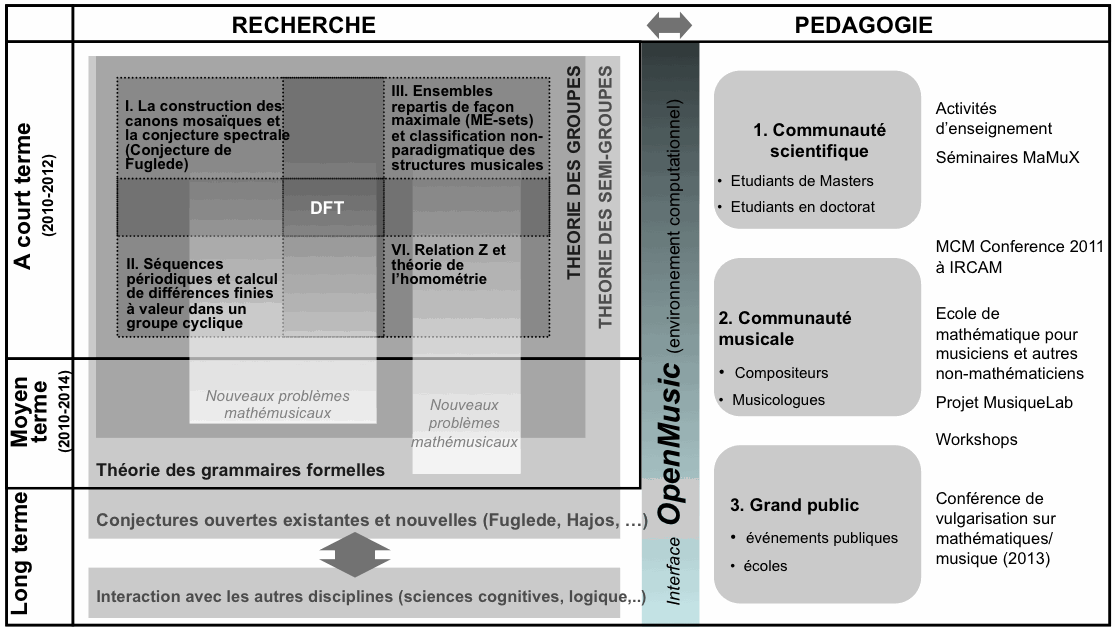
Fig. 8 : Schéma détaillant l’articulation entre activités de recherche et activités pédagogiques dans le domaine des rapports entre mathématiques et musique, telles que nous l’avons proposée dans le cadre du projet MATHnMUSIC.
En ce qui concerne les objectifs de l’activité de recherche pour les quatre prochaines années, il s’agira de se focaliser sur quelques problèmes mathémusicaux majeurs sur lesquels nous avons travaillé jusqu’à présent en essayant, d’un côté, de les étudier à l’aide de la transformée de Fourier discrète et ensuite de généraliser l’approche basée sur la théorie des groupes à l’aide de structures algébriques plus générales, telles les semi-groupes. L’enjeu principal est celui d’intégrer des problèmes mathémusicaux existants et des nouvelles conjectures mathématiques posées par la musique à l’intérieur de la théorie des grammaires formelles. Ceci devrait permettre de mieux comprendre l’interaction du noyau MaMu (Mathématiques/Musique) avec les autres disciplines, telles les sciences cognitives, la logique et la philosophique.
En particulier, en ce qui concerne les retombées cognitives et perceptives du rapport mathématiques/musique, nous allons reprendre les objectifs du projet " Mathématiques/Musique & Cognition ", qui va être intégré formellement au sein des activités de recherche de l’équipe Représentations Musicales. Nous avançons l’hypothèse selon laquelle le manque d’intérêt de la part de la psychologie expérimentale, des sciences cognitives et des neurosciences pour les approches mathématiques en analyse et composition musicales relève d’une difficulté dans le dialogue multidisciplinaire. Force est de constater que la communauté des " musicologues computationnels " et celle des " musicologues cognitifs " n’ont jamais véritablement essayé de réfléchir aux enjeux communs de leur activité de recherche. Nous avons pour objectif principal pour les quatre prochaines années d’essayer de créer des conditions favorables pour ouvrir un véritable dialogue multidisciplinaire entre ces deux orientations majeures de la musicologique systématique d’aujourd’hui en s’appuyant sur une collaboration nouvelle entre la recherche " mathémusicale ", l’informatique et les neurosciences cognitives (Fig. 9).
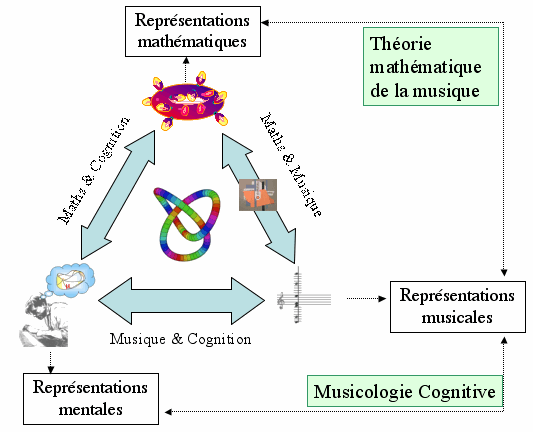
Fig. 9 : Schéma détaillant les rapports possibles entre " Théorie mathématique de la musique " et " Musicologie Cognitive " au sein d’une articulation plus générale concernant les mathématiques, la musique et la cognition.
Dans son analyse consacrée aux liens entre mathématiques et neurosciences [19], Alain Berthoz propose une vision des mathématiques qui s’applique tout à fait à la problématique que nous souhaitons développer. Si c’est indéniable que les mathématiques ont souvent été les protagonistes des tournants scientifiques en contribuant au même temps à des changements de paradigmes dans la connaissance (de l’invention du calcul infinitésimal à la géométrisation de la physique [20]), on peut imaginer que " dans les rapports des mathématiques aux sciences du vivant et de la cognition, nous sommes face à la possibilité d’un tournant comparable. Les neurosciences y sont au centre. Les enjeux sont si importants et originaux qu’il faut s’attendre à des changements de paradigme de grande envergure " (ibid., p. 178). On peut donc renverser la perspective traditionnelle, bien résumée par le mot du physicien Eugène Wigner quand il souligne " la déraisonnable efficacité des mathématiques " et partir des sciences cognitives, et en particulier des neurosciences intégratives, pour voir quels types de problèmes nouveaux se posent aux mathématiques, notamment via la musique. En effet, si d’un côté les mathématiques ont trouvé de plus en plus d’applications dans les neurosciences intégratives et cognitives, dans les dernières décennies, pour reprendre l’analyse de Berthoz, " les progrès dans ces disciplines sont en train d’enrichir les conceptions classiques de l’origine, des fondements et de la nature des mathématiques et de susciter des avancées nouvelles en mathématiques " (ibid., p. 177).
Bien que nous soyons encore loin de pouvoir imaginer un tel renversement de perspective à partir des problèmes posés par la cognition et perception musicale, nous avons déjà pu constater dans quelle mesure les mathématiques constituent un cadre privilégié pour l’étude de certaines fonctions cérébrales intégrées. Nous avons en effet consacré une journée d’étude à un sujet n’ayant pour l’instant aucune application directe dans la musique à savoir la modélisation de l’activité neuronale à l’aide de la théorie mathématique des catégories. Ce modèle appelé " Systèmes Evolutifs à Mémoire " (ou SEM), est le fruit d’une collaboration entre une mathématicienne et un médecin. Andrée C. Ehresmann et Jean-Paul Vanbremeersch ont développé ensemble à partir des années 1980 ce modèle théorique initialement pour des systèmes naturels complexes tels les systèmes biologiques, sociaux ou culturels, et ensuite pour les systèmes cognitifs (modèle MENS pour Memory Evolutive Neural Systems). C’est ce dernier modèle qui a fait l’objet d’une journée d’étude qui a montré, de façon plus générale, la pertinence de la théorie des catégories pour l’étude des systèmes dynamiques. C’est un point qui mérite d’être souligné, car on reproche souvent à cette théorie de négliger l’aspect temporel en privilégiant la notion de structure sur l’idée de processus [21]. La question sous-jacente au modèle MEMS est celle de l’émergence des processus d’ordre supérieur du fonctionnement du cerveau ce qui découle de la modélisation des objets mentaux par des cat-neurones (neurones de catégorie), liant une multiplicité d'hyper-assemblées de neurones. Grâce à la modélisation catégorielle, il est possible de donner une formalisation du concept d’émergence, étroitement liée au processus de " complexification " par liage et classification (via colimites et limites projectives). Le modèle MENS montre comment des objets de complexité croissante peuvent émerger par une suite de complexifications, dès lors qu'un certain " principe de multiplicité " (ou degeneracy dans le sens de G. E. Edelman est vérifié.
Comme les auteurs l’ont souligné dans leur présentation détaillée du modèle MENS, ceci conduit à une " algèbre des objets mentaux " (au sens de Changeux), ce qui mène à la formation d'un invariant global, le noyau archétypal, confirmé par la découverte récente, dans le cerveau, du neural connection core [22]. Ce noyau archétypal intègre les expériences saillantes et/ou régulièrement ré-enforcées, à la fois sensitives, motrices, émotionnelles, procédurales et sémantiques. Ce sont des questions qui nous semblent pouvoir ouvrir des perspectives nouvelles dans l’étude de la cognition et perception musicales. Nous envisageons dans la suite des activités de ce groupe de travail la mise en place d’un protocole de recherche étudiant les processus cognitifs ainsi que les corrélats neuronaux du modèle MENS appliqué à la musique. Ceci touche à la fois à la notion de représentation géométrique et catégorielle des structures musicales mais aussi au concept même d’espace musical dont nous proposons d’étudier les rapports avec les neurosciences en s’appuyant sur les recherches les plus récentes autour de la réalité virtuelle [23].
On aurait ainsi une piste nouvelle pour aborder les retombées cognitives et perceptives de l’un des axes de recherche du projet MISA (Cf. section A.2.1), à savoir le paradigme transformationnel en analyse musicale, à la fois dans la version de David Lewin mais aussi dans la démarche inaugurée par Henry Klumpenhouwer avec les K-réseaux (ou K-nets). En effet, si le paradigme " set-théorique " classique en analyse musicale repose finalement sur l’idée d’un catalogage de l’espace combinatoire des structures de hauteurs (ou rythmiques) présentes dans une partition analysée [24], l’analyse transformationnelle implique un double mouvement. D’un côté on vise la " construction " d’une configuration abstraite d’objets musicaux (appelée " réseau transformationnel ") mais également, d’un autre côté, l’" utilisation " de cette architecture formelle permettant de dégager des critères de pertinence pour la réception de l’œuvre et pour son interprétation. Autrement dit, l’intérêt de construire un réseau réside dans la possibilité de l’utiliser, à la fois pour " structurer " l’écoute par rapport à la singularité de l’œuvre analysée mais également pour établir des critères formels qui pourront servir pour aborder le problème de son interprétation. La construction d’un réseau transformationnel ou bien d’un K-réseau s’appuie, en effet, sur une volonté implicite de l’analyste de rendre " intelligible " une logique musicale à l’œuvre dans la pièce analysée. Cette démarche analytique possède à notre avis des implications théoriques tout à fait nouvelles pour les sciences cognitives, comme le suggère un rapprochement direct entre la théorie transformationnelle en analyse musicale et des nouveaux courants de la psychologie du développement, en particulier le néostructuralisme de Halford et Wilson [25] et ceux qu’Olivier Houdé appelle les " derniers ajustements piagétiens [26] " dans une approche catégorielle de l’épistémologie génétique.
D’autres questions ouvertes, que nous nous proposons d’aborder dans les travaux futurs, concernent la pertinence des algèbres de dimension supérieure comme outils descriptifs et opérationnels tout d’abord en neurosciences [27] et ensuite dans le domaine de la cognition et perception musicales. On pourra également étudier la pertinence du transfert vers la musique d’une théorie générale du sens qui a été développé par René Guitart [28] à la suite des travaux d’Ehresmann et Vanbremeersch sur les systèmes évolutifs à mémoire, dont nous avons mentionné les liens conjecturaux avec la musique (cf. supra). Ceci permettrait, plus à long terme, d’arriver à constituer un cadre conceptuel pour l’étude des relations entre mathématique/musique et cognition dans lequel pouvoir aborder des notions qui ont été traditionnellement associées à une démarche sémiotique, telle la notion du " sens " en musique, mais cette fois de façon indépendante de toute considération sur le langage et son rapport avec la musique.
Si l’étude des ramifications cognitives des algèbres de dimension supérieure constitue l’un des objectifs à long terme, l’utilisation de la transformée de Fourier discrète (DFT) dans la modélisation algébrique des structures musicales semble constituer une démarche très prometteuse. L’objectif des quatre prochaines années sera donc d’étudier en détail cette utilisation, en proposant des batteries de tests expérimentaux pour étudier les retombées perceptives d’une telle formalisation. Cette recherche sera menée en collaboration étroite avec des mathématiciens (tels Emmanuel Amiot et John Mandereau) ainsi que des chercheurs de l’équipe " Espaces acoustiques et cognitifs " de l’Ircam (en particulier Isabelle Viaud-Delmon).
NOTES :
[1] Une description plus exhaustive des problèmes " mathémusicaux " sur lesquels j'ai travaillé jusqu'à présent, incluant également la théorie des block-designs ainsi que la théorie des séquences périodiques et le calcul de différences finies à valeur dans un groupe, est contenue dans le mémoire d'HDR intitulé " Mathematica est exercitium musicae : la recherche 'mathémusicale' et ses interactions avec les autres disciplines ", en préparation).
[2] D. Lewin, " Making and Using a pcset Network for Stockhausen's Klavierstück III ", Musical Form and Transformation: 4 Analytic Essays, New Haven: Yale University Press, 1993, p. 16-67.
[3] G. Mazzola, M. Andreatta, " From a categorical point of view : K-nets as limit denotators ", Perspectives of New Music, vol. 44, n° 2, Août, 2006, p. 88-113.
[4] G. Mazzola et M. Andreatta, " Diagrams, gestures and formulae in music ", Journal of Mathematics and Music, Vol. 1, No. 1, Mars 2007, p. 23-46.
[5] Cette intervention, qui a été enregistrée par la Diffusion de savoir de l'ENS, a été reprise dans le cadre d'un article à paraître dans un numéro spécial de la revue de Synthèse (sous la direction de Ch. Alunni, M. Andreatta et F. Nicolas).
[6] Les fiches en version bilingue (français et anglais) du glossaire sur la Set Theory sont disponibles en ligne à l'adresse : http://www.termisti.refer.org/data/settheory/settheoryhome.html
[7] M. Andreatta, Gruppi di Hajos, canoni e composizioni, tesi di laurea, département de mathématiques, Université de Pavie, 1996.
[8] Voir en particulier l'adresse : http://recherche.ircam.fr/equipes/repmus/mamux/IrcamTilingResearch.html
[9] Un sous ensemble H d'un groupe G est périodique si il existe un élément non nul g G, tel que g+H=H, ou bien, ce qui est équivalent, s'il existe un sous-groupe normal (non vide) K de G tel que K+H=H.
[10] J. Rosenblatt, " Phase Retrieval ", Communications in Mathematical Physics 95, 1984, p. 317-343.
[11] Voir le mémoire de Master ATIAM de John Mandereau.
[12] Plus d'information sur la collection " Musique/Sciences " à l'adresse : http://www.ircam.fr/598.html
[13] Plus d'information sur la collection " Computational Music Sciences " à l'adresse : http://www.springer.com/series/8349
[14] Un bilan détaillé des huit
premières séances du séminaire (années
2001-2009) incluant la liste complète des participants,
est disponible à l'adresse :
http://recherche.ircam.fr/equipes/repmus/mamux/BilanSemMaMuX2001-2009.html
[15] Les enregistrements de la plus grande partie des séances, ainsi que la liste complète des intervenants, sont disponibles à l'adresse : http://www.entretemps.asso.fr/maths/.
[16] Les enregistrements et les textes des différentes séances de l'école sont disponibles à l'adresse : http://recherche.ircam.fr/equipes/repmus/mamux/EcoleYA.html
[17] Le rapport du groupe de travail " Mathématiques/Musique & Cognition " est disponible à l'adresse : http://recherche.ircam.fr/equipes/repmus/mamux/Cognition.html
[18] Pour plus d'informations sur ce projet, voir à l'adresse : http://recherche.ircam.fr/equipes/repmus/mamux/PEPS-GdIM.html
[19] A. Berthoz, " Les liens entre mathématiques et neurosciences ", dans Les mathématiques dans le monde scientifique contemporain, Académie des sciences, rst n° 20, 175-211, 2005. Avec la complicité de Daniel Andler, Daniel Bennequin, Jacques Droulez, Olivier Faugeras, Giuseppe Longo, Stéphane Mallat et Jean Petitot.
[20] Et, on ajoutera, également de la
logique et de l'informatique, un sujet qui a eu une forte expansion
dans les dernières années et dont les retombées
dans le domaine de la cognition constituent un terrain très
riche pour la recherche interdisciplinaire. Voir à ce propos
notre projet exploratoire " Géométrie de l'Interaction
et musique ", retenu dans le cadre des interactions Maths-ST2I
: http://recherche.ircam.fr/equipes/repmus/mamux/PEPS-GdIM.html
[21] Notons également que cette orientation
" dynamique " propre à l'approche catégorielle
a ouvert une nouvelle perspective dans la théorie mathématique
de la musique de Guerino Mazzola. Si Topos of Music (Mazzola,
2002) est la summa de ce qu'on peut théoriser des
aspects " hors temps " de la musique, pour reprendre
la terminologie de Iannis Xenakis, d'autres constructions mathématiques
se sont avérées nécessaires pour rendre compte
du caractère continu de la notion de " geste "
en musique. Comme dans le cas des systèmes évolutifs
à mémoire, la théorie mathématique
des gestes (cf. Section A.2.1 a) s'appuie sur une paramétrisation
temporelle des structures catégorielles, ce qui pourrait
avoir à son tour des retombées intéressantes
en sciences cognitives.
[22] Voir Hagmann, P., Cammoun, L., Gigandet,
X., Meuli, R., Honey, C.J., Van J. Wedeen & Sporns, O., "
Mapping the Structural Core of Human Cerebral Cortex ", PLoS
Biology 6, Issue 7, p. 1479-1493, 2008. Online: www.plosbiology.org
[23] Viaud-Delmon I., Réalité virtuelle, integration
multi-sensorielle & espace : de l'outil expérimental
au paradigme scientifique, mémoire d'habilitation à
diriger des recherche, Université de Paris VI, 2006.
[24] Et donc, in fine, à l'idée de symétrie et au concept d'invariance. Symétrie et invariance sont intimement liées à la structure mathématique de groupe, si bien qu'étudier la perceptibilité de la notion de symétrie et d'invariance en musique revient à étudier les effets cognitifs de l'action d'un groupe de transformation sur une structure musicale donnée.
[25] Halford G. S. et Wilson W. H., " A category-theory approach to cognitive development ", Cognitive Psychology, 12, p. 356-411, 1980.
[26] Houdé O. et Miéville D., Pensée Logico-mathématique, nouveaux objets interdisciplinaires, Paris, Presses Universitaires de France, 1993. Voir aussi E. Acotto et M. Andreatta, " Représentations mentales musicales et représentations mathématiques de la musique ", à paraître dans InCognito, Cahiers Romans de Sciences Cognitives, Vol. 4, No. 3, Déc. 2009.
[27] Brown R. & Porter T., " Category Theory and Higher Dimensional Algebra : potential descriptive tools in neurosciences ", 2008 (online : http://arxiv.org/pdf/math/0306223v2).
[28] Guitart R., " Théorie du nouveau
", intervention dans le séminaire mamuphi,
école normale supérieure, 9 mai 2009. Argumentaire
de la séance et texte préparatoire disponibles à
l'adresse : http://recherche.ircam.fr/equipes/repmus/mamux/MamuPhiXMai09.pdf
[Mise à jour : février 2010]